Tolerance Testing

Navigation: User Guide ➔ Solver ➔ Tolerance Testing

Project, Model and Solver Settings				Simulation Modes and Solver Setup			Solver Methodology, Convergence and Tolerance				Solving Models
Project Settings	Solver Settings	Plant Model	Constants	Simulation Modes	ProBal Setup	Dynamic Setup	Solver Status	Solver Methodology	Convergence Methods	Tolerance Testing	Evaluating Sub-Models	Flash Train	Mass & Energy Balance	Referenced Variables	Demand

Related Links: Audit

---

Introduction

For the solver in a SysCAD project, there are many different calculations that need to be solved to an appropriate degree of accuracy. We need to calculate an error and use tolerances to determine when iterative calculations are considered to be converged. Below we describe the theory and a more general detailed description of how SysCAD performs these calculations using tolerances.

Theory

In SysCAD a few different methods are used for testing for convergence using tolerances. Most commonly a Normalised Relative Error is used, which is a calculation using both a Relative and Absolute Tolerance setting for comparing two numbers. The solver recycle tears are an important example that use this method.

We have:

• [math]\displaystyle{ V_1 }[/math] and [math]\displaystyle{ V_2 }[/math] Measured, Previous or Target Values in SysCAD SI Units
• [math]\displaystyle{ e_a = V_1-V_2 }[/math] Absolute error
• [math]\displaystyle{ M = \max(|V_1|, |V_2|) }[/math] Maximum of the absolute values of the two values
• [math]\displaystyle{ e_r = \frac{V_1-V_2}M }[/math] Relative error
• [math]\displaystyle{ \epsilon_r }[/math] relative tolerance
• [math]\displaystyle{ \epsilon_a }[/math] absolute tolerance
• [math]\displaystyle{ e_N = \frac{|V_1 - V_2|}{\epsilon_a + \epsilon_r M} }[/math] Normalised relative error
• [math]\displaystyle{ Converged = e_N \lt 1 }[/math] Test for converged (close enough) state

The normalised error must be less than 1.0 for the variable to be converged. This guarantees that either the absolute error is less than the absolute tolerance, or the relative error is less than the relative tolerance, in particular it deals with the situation when a variable is very small or zero.

Changing the relative tolerance from 0.01 to 0.1 would increase the error margin by an order of magnitude. Typically the relative tolerance would be greater than or equal to the absolute tolerance used.

Notes:

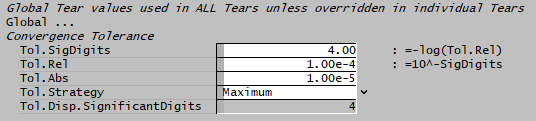
• We can represent the Relative Tolerance ([math]\displaystyle{ \epsilon_r }[/math]) as a number of significant digits, where [math]\displaystyle{ SigDigits = -log(\epsilon_r) }[/math]
• If the measured values ([math]\displaystyle{ V_1 }[/math] and [math]\displaystyle{ V_2 }[/math]) are significantly larger than the absolute tolerance ([math]\displaystyle{ \epsilon_a }[/math]) then the contribution of the absolute error is insignificant and the Relative error is approximately equal to the Normalised relative error multiplied by the Relative error ( [math]\displaystyle{ e_N * \epsilon_r \approx e_r }[/math] ).
• In addition to use for testing solver convergence criteria for tears and PIDs, this method of using a normalised relative tolerance test is used extensively within the Reaction Block (RB) and other parts of SysCAD unit models and sub-models.
• The normalised relative tolerance test is used for various reporting checks and condition warnings. A good example of this is in the Audit checks and reporting.
• Many individual units may have iterative convergence calculations that do not use the full normalised relative tolerance tests described here. They may simply test against an absolute tolerance only ([math]\displaystyle{ |e_a| \lt \epsilon_a }[/math]), or relative tolerance only ([math]\displaystyle{ |e_r| \lt \epsilon_r }[/math]). In these cases, the problems of very small numbers or target value of zero are not applicable.
• Many individual units use the Brent solver to determine convergence. Please see Solver Setting - Tolerances for a description of the Brent convergence routine and some examples of the tolerances for various system solver tools.

Overview Discussion

Any calculations you do, whether with pencil and paper, slide rule, pocket calculator or computer, will never be exact. This is not a problem, since measurements of plant parameters are not exact either. A highly accurate thermocouple will give a temperature to within 0.1 degrees of the the actual value, mass flow, pressure and compositions can only be determined to within some error.

When we set up a PID controller to regulate temperature in a real plant (say by controlling steam flow as in the introductory tutorial), we are happy if we get the temperature to within 0.1°C of the setpoint, after all, if we can't measure the temperature to better than this accuracy, then there is no point in controlling the flow to a higher precision.

In SysCAD, we can calculate things to a much higher degree of accuracy, but there is an ultimate limit: our computer can only represent values to a finite number of decimal places. A floating point number can have about 16 decimal places of accuracy (we will discuss exactly what this means and where it comes from shortly) So our upper limitation on accuracy is the precision of our representation of floating point numbers.

Much of what we do in SysCAD involves iterative or computationally expensive calculations. Suppose we are trying to regulate steam flow to achieve a particular temperature (as above). We could in theory have an exact calculation for this, if we had analytic expressions for specific heat and enthalpy for steam and the process fluid being heated, but even then we would be limited by the floating point precision. In practice we revert to numerical techniques - root finding - for solving this sort of model. We have a function [math]\displaystyle{ T = f(Q) }[/math] where Q is the steam flow, and T is the autoclave temperature, and we solve the equation [math]\displaystyle{ e = T_r - f(Q) = 0 }[/math] for the value of [math]\displaystyle{ Q }[/math] to give us the desired temperature. We don't generally want an exact value accurate to 17 decimal places such that changing the final decimal place by 1 up or down will give us a greater error; instead we are happy that the error is less than some tolerance. One millionth of a degree should be good enough for us - this is somewhere between the accuracy we can achieve in plant measurement (0.1°C), and the floating point precision (about a millionth of a nano-Kelvin). Also, all those extra decimal places translate into a lot more computational effort (which means slowing down the speed at which SysCAD solves the model, and who wants to wait).

This measurement (the difference between the desired (or target) number, and the actual number from solving the equation, is called the absolute error.

[math]\displaystyle{ e_a = V - V_t }[/math]

We then pick a small number [math]\displaystyle{ \epsilon }[/math] as our tolerance (mathematicians, computer scientists and engineers will understand [math]\displaystyle{ \epsilon }[/math] represents a tiny numbers). Tolerance turns up everywhere in engineering and manufacturing. When machining a component such as a shaft, we might have a tolerance of a few micron, while navigating to a particular point using GPS, you are happy with a tolerance of several meters. The tolerance depends on the situation.

OK, so if our absolute error is one millionth ([math]\displaystyle{ \epsilon = 10^{-6} }[/math]), we should be happy, right? But suppose we are looking at gold or rare earth production, where the flows of important trace elements may just be a few grams an hour. A gram an hour is a thousandth of a kilogram an hour, and less than a millionth of a kg per second, which is the SI unit for mass flow, so an absolute error of a millionth is going to be of the same order as the actual value.

So what really matters is not what the absolute error is, but what is the error compared to what we expect the result to be. We call this the relative error. Given a target value [math]\displaystyle{ V_t }[/math] and a value [math]\displaystyle{ V }[/math] we calculate one way or another, we define our relative error as

[math]\displaystyle{ e_r = \frac{V - V_t}{V_t} }[/math]

In other words, we scale the absolute error by the target value. Good to go, right?

Well no, we have a further complication. There are situations when the target value is zero, so the previous equation makes no sense. (In setting up the makeup controller in the tutorial, our "target" was to have zero acid in the product stream. So as to avoid dividing by zero (generally a bad idea with computers) we modify the equation by having the denominator not the target, but the maximum of the target and the value (or actually the absolute values of these, since sometimes our target will be negative).

[math]\displaystyle{ e_r = \frac{V - V_t}{\max(|V|, |V_t|)} }[/math]

(We understand here that if both values are zero, then the relative error is zero as well.) We have avoided dividing by zero, but there is still a problem. If the target is zero, the relative error is always going to be 1. So what to do - we should really be using the absolute error in this case.

So both absolute and relative errors have problems. What to do? The answer is to have both relative [math]\displaystyle{ \epsilon_r }[/math] and absolute tolerances [math]\displaystyle{ \epsilon_a }[/math] and combine them in a special way. We define a normalised relative error as

[math]\displaystyle{ e_N = \frac{|V - V_t|}{\epsilon_a + \epsilon_r\max(|V|, |V_t|)} }[/math]

Our close-enough condition is that our normalised error [math]\displaystyle{ e_N \lt 1 }[/math]. This subsumes both the relative and absolute conditions we discussed above. If the absolute error is less than the absolute tolerance then the denominator is greater than the absolute error, so the condition holds. If the relative error is less than the relative tolerance then the same is true. We are happy with either of these conditions holding - we can accept a large relative error provided the absolute error is small in the case when the target is small or zero, and we can accept a large absolute error for large numbers (if we have a production of a million tons a year, then 1kg/hr is not going to be noticed.) We are getting the best of both worlds, albeit at the expense of having two tolerance parameters. Most of the time, when the value of the variable is 'typical' in some sense for plant conditions, the absolute tolerance contribution to the denominator is negligible, and the condition just becomes a relative tolerance. Only when the value is small, does the absolute tolerance become significant.

Whenever a tolerance calculation is required in SysCAD (comparing two values [math]\displaystyle{ V_1 }[/math] and [math]\displaystyle{ V_2 }[/math]), it is usually performed by taking the difference between two values (for example between the current and previous values) and dividing it by a combination of the applicable absolute and relative tolerances as defined above.

Typically the relative tolerance would be greater than or equal to the absolute tolerance used. Internally, SysCAD typically sets an upper limit on the relative tolerance of 1%. A lower limit on absolute tolerance would be the machine precision: this is determined by SysCAD using double precision 64 bit floating point numbers. Of those 64 bits, 53 of them actually determine the decimal places; the remainder determine the magnitude and sign. Since [math]\displaystyle{ 2^{53}\approx 10^{16} }[/math] any more than 16 decimal places of accuracy would be pointless.

One common situation is when we are converging variables in a tear stream - we keep on iterating until the value is "close enough" to the previous value. The values for the tolerance settings for the tear solver can be found in solver settings (and also in the Solver Setup menu dialog).

Examples

1. If the relative tolerance was set to 0.1, and the variable of interest was a mass flowrate with a previous value of 1000 kg/s, then for this variable to be converged the current value would have to be in the range of 900 to 1111 kg/s, i.e. about 10% either side of the previous value.
2. If the relative tolerance was set to 0.01, and the variable of interest was a mass flowrate with a previous value of 1000 kg/s, then for this variable to be converged the current value would have to be in the range of 990 to 1010 kg/s, i.e. about 1% either side of the previous value.
3. The absolute tolerance becomes important when the value of a variable is close to zero. If the relative tolerance was set to 0.1, the absolute tolerance was set to 0.01, and the variable of interest was a mass flowrate with a previous value of 0 kg/s, then for this variable to be converged the current value would have to be less than 0.011 kg/s, i.e. a difference of about 0.01 (=the absolute tolerance) from the previous value.