Falling Film Evaporator 3
Navigation: Models ➔ Energy Transfer Models ➔ Falling Film Evaporator 3
Related Links: Falling Film Evaporator 4, Evaporator
General Description
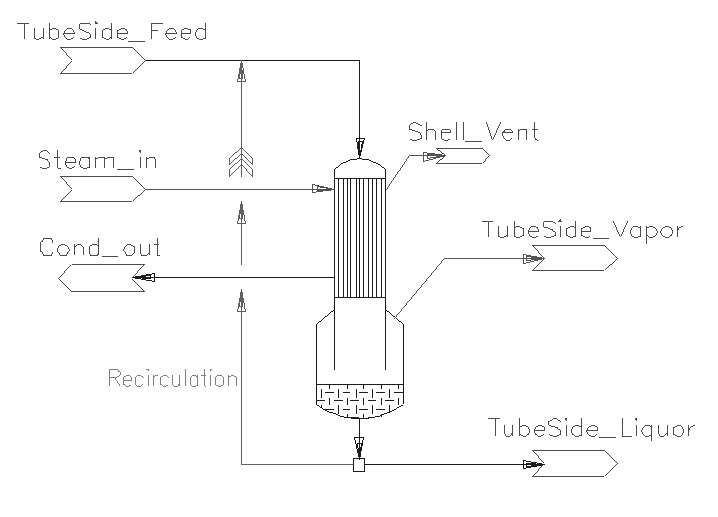
The falling film evaporator 3 (FFE3) is used for to evaporate water from liquor. A schematic of the unit operation and its inlets and outlet are shown in the diagram below.
The unit operation is called a falling film evaporator, but the model is also perfectly applicable to a rising film evaporator - the descriptive equations are the same. The basic layout is a vertical tube bundle in a shell with the liquor to be evaporated on the tube side and heating steam to the shell side. In normal operation there is sufficient heat transfer to heat the tube side liquor to its boiling point and evaporate some water. This greatly enhances heat transfer in the tubes. The mass flow of evaporated steam will be about the same as the heating steam, but it will be at a lower temperature and pressure. Generally it is still useful for other heating applications in the process and exported to a subsequent evaporation stage as heating steam or elsewhere in the process plant. There are many different physical arrangements for feed, volumes, recirculation, etc. The flow of liquor in the tubes may be either downwards or upwards depending on the arrangement.
In a falling film evaporator, weak liquor is pumped to the top of the unit and distributed to the tubes where it runs down as a film. There is often some recirculation of evaporated liquid back to the inlet.
In a rising film evaporator, weak liquor rises up through the tubes - it is driven by the the formation of steam bubbles in the tubes. Some of the liquor is often recycled back to the bottom of the tubes.
The concentrated liquor and vapour streams will leave the system at the specified operating pressure. This is usually the saturation temperature of the product liquor, although if there is not sufficient heat transfer then there will be no evaporation and the liquor will exit at the temperature determined by the heat transfer.
The model includes a number of different options for environmental heat loss which is assumed to come from the shell side. Shell side condensate leaves the system at the saturation temperature based on the shell side operating pressure.
NB: The FFE3 can be connected to a demand source or a flash tank to supply steam to it and SysCAD will automatically control steam flow or flash tank operating pressure to meet steam demand. However, at present if the FFE3 is connected to supply evaporated steam to a heat exchanger or another evaporator, SysCAD is unable to automatically find the tube side operating pressure and the tube side operating pressure must be specified. It is possible to add a PID controller to find the adjust the tube side operating pressure to correctly satisfy all the operating constraints(this is detailed below).
Diagram
The diagram shows a drawing of the Falling Film Evaporator, with the connecting streams. The Falling Film Evaporator requires Steam In and Liquor Feed connection in and Condensate, product liquor and evaporated vapour connections out. There is also an optional vent connection from the shell side for non-condensable removal. The table below shows the minimum and maximum numbers of connections. There can be multiple sources of tube side feed and steam in.
Inputs and Outputs
| Label | Required Optional |
Input Output |
Number of Connections | Description | |
| Min | Max | ||||
| Tube_In | 1 Required | In | 1 | 10 | Weak Liquor |
| Tube_Out | Required | Out | 1 | 1 | Concentrated Liquor |
| Shell_In | 1 Required | In | 1 | 10 | Steam in |
| Shell_Out | Required | Out | 1 | 1 | Condensate out |
| Tube_Vap_Out | Required | Out | 1 | 1 | Evaporated Vapour. |
| Shell_Vent | Optional | Out | 0 | 1 | Optional vent for non-condensables and excess steam. |
Behaviour when Model is OFF
If the user disables the unit, by un-ticking the On tick box, then the following actions occur:
- All streams connected to 'Tube In' will flow straight out of 'Tube Out' with no change in temperature and no evaporation;
- All streams connected to 'Shell In' will flow straight out of the 'Shell Out' with no change in temperature and no condensation;
- There will be no flow to the vent;
- There will be no environmental heat transfer.
The unit will basically be 'bypassed' without the user having to change any connections.
Model theory
There are several different operating modes for the FFE3. The mass flow of steam to the unit may be;
- set manually by the user;
- controlled automatically in demand mode where the FFE3 calculates the amount of steam at the given pressure and temperature that can condense and draws that;
- connected to a flash tank where the amount of steam flashed from the flash tank, the resulting flash pressure and the amount of steam the FFE3 can condense at that pressure are all balanced.
The tube side operating pressure is an input variable (this value may be set either manually or by a PID controller).
The theoretical heat transfer from the shell side to the tube side is calculated based on heat exchange area, heat transfer coefficient (HTC) and temperature difference between the shell side and the tube side (there is an option to use either delta T or LMTD). This is the limiting amount of heat transfer to the tube side that can occur. The actual condensate duty may be higher if there is environmental heat loss.
The steam mass flow to the FFE3 may be higher than the amount that condenses if there is a vent flow specified - the vent flow will include the specified amount of steam plus all non-condensable gases in the steam flow in. The vent flow, concentrated liquor flow and evaporated steam flow are all assumed to be at the same pressure and temperature.
- [math]\displaystyle{ Q=UA \times LMTD\,\,\,\,or\,\,\,\,Q=UA \times \Delta T }[/math]
The amount of evaporated steam from the liquor stream is calculated based on:
- Energy available from the inlet steam which may include superheat and condensation.
- Less environmental heat loss
- Less any energy required to heat the liquor stream to saturation temperature
- Any energy adjustment for vent flow
- Mass of evaporated steam is = Energy available / latent heat (Final Liquor T, P)
Operation Discussion
General behavior
Falling film evaporators are a combination of flash tanks and heat exchangers. Their operation has subtleties that combine issues associated with both. In addition they are often connected in series with other evaporators or other flash tanks and the behavior of the whole system may be yet again more complex.
Some of the behavior may be counter-intuitive. For example;
- unlike a normal heat exchanger, it is possible for the temperature of the feed liquor stream to rise or fall, depending on the tube side pressure. Hot tube side liquor may flash to a colder temperature if the tube side pressure is low enough.
- it is possible for the unit to have steam condensing on the shell side even when the feed liquor temperature is higher than the steam saturation temperature. This is because the final liquor temperature is determined by the tube side operating pressure, and the temperature after flashing may be lower than the steam saturation temperature.
In such cases, recirculation is often used to maintain a lower tube side temperature. Recirculation takes colder product liquor from the outlet and mixes it with the incoming feed liquor to reduce its temperature. Recirculation is also used in operation to increase tube side velocities to increase the tube side heat transfer coefficient and reducing scaling.
A good understanding of the operating principles of evaporators is helpful in constructing and debugging models.
Steam Connection Type
There are three different connection modes for steam supply to the FFE3. The mode is selectable in the access window for the FFE3 and allows the FFE3 unit operation to be configured for different applications or situations.
- Manual - No Demand In manual mode the supply of steam to the FFE3 is controlled externally to the model. This can be user set or controlled by a PGM or PID controller. There is no limit on the amount of steam that can be sent to the model. However, if the steam supply exceeds the theoretical steam demand, the model will only condense an amount to meet the theoretical demand and the excess will be sent to the vent and an excess steam warning will be issued. This mode is used to model situations when there is not enough steam available to meet the theoretical demand or where the steam supply is intentionally controlled.
- General Demand Mode This is a demand mode where the steam mass flow is determined by the heat exchanger configuration, operating parameters and liquor stream flow. There must be a demand source connected to the steam line into the FFE3. The FFE3 will calculate how much steam could theoretically be condensed in the unit for the given area, HTC, liquor flow, heat loss and venting and the demand will be passed to the demand source which will then supply the required steam. This mode is useful when the FFE3 is connected to a plant steam supply for example the first effect in a multiple effect evaporator train or when a single unit is being used.
- Flash Train Mode In this mode the FFE3 is connected to a flash tank which supplies steam to the shell side for heating. SysCAD recognizes the flash tank and the FFE3 as being connected and creates a macro model with the pair. In operation, as the flash tank pressure is reduced, more steam is flashed. However, the saturation temperature of that steam reduces with pressure and thus there is less driving force for heat transfer in the FFE3 and this reduces the theoretical heat transfer. The macro model solves by adjusting the flash pressure so that everything balances - the steam flashed has exactly the right saturation temperature to meet the theoretical demand in the FFE3.
Operating Pressure
The shell side operating pressure cannot be higher than the steam supply pressure, but pressure drop can be controlled. The FFE3 has three options for shell side pressure control.
- None There is no pressure control and the shell side operating pressure is the same as the supply pressure.
- Set Shell Pressure The shell side operating pressure can be controlled to a fixed pressure (that is less than the supply pressure). This allows temperature rise or steam production rate to be controlled.
- Set Shell delta P The shell side operating pressure will be the steam supply pressure minus a specified pressure drop. If the supply pressure changes, the operating pressure will track the change minus the pressure drop. This allows steam system and steam valve pressure drops to be modeled and also allows for control of the unit. For example a PID can be used to control pressure drop to give a target evaporation rate.
The Tube Side Operating Pressure is an input variable that can be set by the user or a PID or PGM controller. In practice, the tube side operating pressure is generally controlled by the down stream steam demand - often another evaporation effect, condensing heat exchanger, barometric condenser or export to a steam line at a regulated pressure. At present the FFE3 tube side operating pressure cannot be automatically controlled by using the macro model and an external control must be used to adjust the pressure. This feature will be added in a future version. Until this is implemented tube side pressure can be adjusted to match the demand using a PID controller. This method is detailed in a later section.
Flowchart
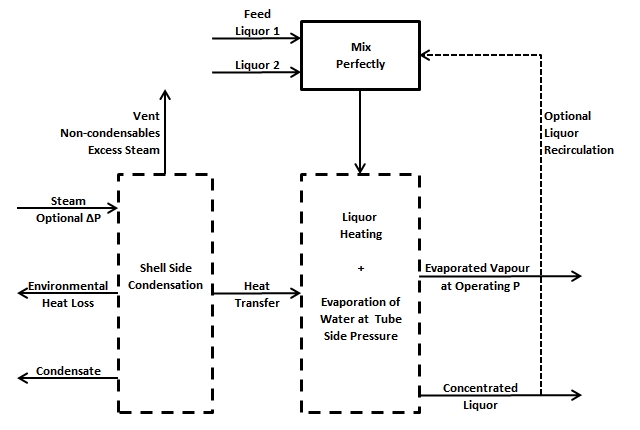
The flow chart below shows the layout of the FFE3. Supply steam enters the shell side with an optional pressure drop. Any non-condensables in the steam plus a user specified vent flow of steam plus any excess steam which cannot be condensed leave through the vent. The theoretical amount of steam that can condense is that required for the maximum calculated heat transfer plus the environmental heat loss. Environmental heat loss is assumed to come from the shell side. The steam condenses at the saturation temperature corresponding to the shell side operating pressure. The condensate and vent streams leave at the same temperature and pressure (NB if the steam supply is superheated, the superheat energy will have been given up for heating and is included in the energy balance). The tube side liquor feed streams are assumed to mix perfectly along with any recirculation flow. The mixed stream enters the tubes and absorbs heat from the shell side. If the liquor is colder than the saturation temperature for the tube side operating pressure, it is heated and once it reaches saturation evaporates water as per the energy balance. The concentrated product liquor leaving the tubes may have some fraction of it recirculated back to the liquor feed. In the FFE3 model there is a built in recirculation option and an external splitter and lines are not required although may be used if desired. The tube side vapor may have some superheat due to boiling point elevation depending on the concentration of solutes in the liquor stream. If this is the case there is an option to remove superheat through environmental heat loss from the tube side so that the exit stream is saturated vapor.
Tube Pressure Control
When the FFE3 is connected to another unit operation which uses steam, the tube side operating pressure must be adjusted so that the exported steam at the specified pressure (which also determines the temperature and mass flow) matches the demand. SysCAD creates macro models for a flash tank and condensing heater but that functionality is not yet implemented for the FFE3 so the user must add an external control to adjust tube side pressure.
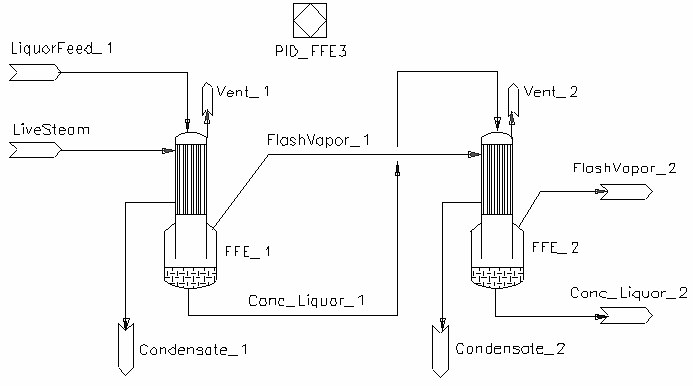
The simplest way to do this is to use a PID controller which uses the theoretical duty of the steam demand (shell and tube heater or another FFE3) as the set point and the actual condensate duty as the measured value. The output or controlled variable is the tube side operating pressure. In the example below there are two FFE3's connected together in series. The first uses live steam to the shell side for heating. The second uses evaporated steam from the tube side of the first one for shell side steam. The concentrated liquor from the first one is the feed for the second one. A multiple effect evaporator train with more effects would have subsequent effects connected in the same way as the second one here except the last effect would be connected to a barometric condenser.
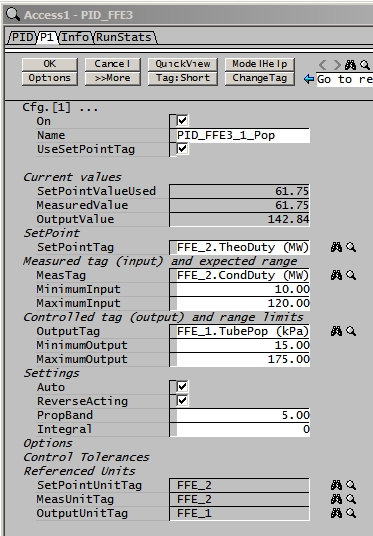
The image of the controller below shows how the actual and theoretical duties of FFE3 number two are used to control the operating of FFE3 number one. Note that the controller is ReverseActing - as the operating pressure (output variable) is increased, the actual condensate duty (measured variable) decreases. This is because, even though the exported steam from the number one evaporator is hotter when operating pressure increases, there is less of it and thus less heat transfer. Conversely when the pressure decreases, there is more steam produced, but saturation temperature goes down and the temperature difference to drive heat transfer decreases so the theoretical steam demand decreases.
NB When setting up these controls in a model it is important to make sure that the input and output ranges make sense and properly span the expected values.
Data Sections
The default access window consists of 5 sections,
- FFEvap3 tab contains general information relating to the unit.
- Results - This second tab contains unit results for the shell and tube side.
- VLE tab - Contains the VLE information for the tube side.
- VLESS tab - Contains the VLE information for the shell side.
- Info tab - contains general settings for the unit and allows the user to include documentation about the unit and create Hyperlinks to external documents.
- Links tab, contains a summary table for all the input and output streams.
- Audit tab - contains summary information required for Mass and Energy balance. See Model Examples for enthalpy calculation Examples.
Falling Film Evaporator 3 Page
Unit Type: FFEvap3 - The first tab page in the access window will have this name.
|
Tag / Symbol |
Input / Calc / Options |
Description |
Requirements | ||
| On | tick box | If this option is switched off, then the unit operation will behave like a pipe model. Thus, inlet conditions = outlet conditions and no heat transfer will take place. |
| DemandConnection | None | Steam flow to the unit is controlled externally to it and it receives whatever is sent to it. |
| FlashTrain | The FFE3 is connected to a flash tank and SysCAD sets up a macro model to automatically control the flash pressure and the flow of steam to the FFE3. The steam flow will be the maximum that the FFE3 can condense for the given operating conditions. However, the operation can be controlled by adding a pressure drop to the shell side steam which will reduce the theoretical heat transfer. See Operating Modes Discussion | |
| GeneralDemand | In this mode the FFE3 is connected to a demand source and will be supplied with all the steam it can condense for the given operating conditions (assuming this does not exceed the maximum supply). Once again shell side operating pressure or pressure drop can be used to control the FFE3. See Operating Modes Discussion | |
| SetShellPressure | Tick box | Only visible with the Live Steam Method. This enables the user to set the shell pressure. |
| ShellPressureControl | None | Shell side steam pressure is the same as the steam supply pressure. |
| Set Shell Pressure | Steam inlet pressure is adjusted to the set shell side pressure. Set pressure variable is ShellSetP. NB this pressure must be equal to or less than the steam supply pressure. Pressure change is adiabatic, isenthalpic process. | |
| Set Shell delta P | Steam inlet pressure is dropped adiabatically and isenthalpiclly by the specified delta P. The delta P variable is ShellSetdP. NB this must be a positive number. | |
| TubeOperatingP | Input | The operating pressure for the tube side. |
| DeltaT_Mode | Tickbox | When ticked, the heat transfer is calculated based on the delta T (shell side saturation temperature - tube side outlet temperature) and when unticked, heat transfer is based on LMTD. |
| HTC | Input | The user specified heat transfer coefficient. |
| Area | Input | The user specified heat transfer area. |
| AddedHeat | Input | The user specified additional heat. |
| POut | Input | The user specified output pressure of the FFE. (Liquor Side) |
| PShell | Input | Only visible with the Live Steam Method and Set Pressure tick box selected. This is the user specified Shell Pressure, the Shell Pressure must be <= steam supply pressure. Used here to act as pressure drop in the shell side. This will affect the condensate outlet temperature and heat exchange with the tube side. Can be used to control the outlet Temperature for the FFE. |
| ReportToleranceQm | Input | Only visible with the Live Steam Method. The required tolerance for error condition messages for matching VapourFlow.Reqd when DemandMode is selected. |
| ReportToleranceDuty | Input | Only visible with the Condensing Method. The required tolerance for warning condition messages when matching Duty. |
| Recirculation of Liquor | ||
| Recirc | Tick Box | This enables the recirculation option. |
| RecircFraction | Input | Only visible if the Recirc option has been selected. The user specified recirculation fraction. The recirculation fraction = Recirculation Flow/(Liquor Product + Recirculation Flow) |
| User Set Limit Warnings | ||
| TubeSideDeltaT | Tick Box | This enables the tube side change in temperature warning. |
| MaxTubeSide_dT | Input | Only visible if TubeSideDeltaT is selected. The user specified maximum tube side change in temperature before a warning is generated. |
| SpecificVapLoad | Tick Box | This enables the specific vapour load warning. |
| MaxVapPerArea | Input | Only visible if SpecificVaporLoad is selected. The user specified maximum specific vapour load (flow of vapour per unit area) before a warning is generated. |
| Show Liquor Side Flows | ||
| ShowQLiqFeed | Tick Box | QLiqFeed and associated tab pages (e.g. Qm) will become visible, showing the properties of the combined fresh liquor feed stream. See Material Flow Section. |
| ShowQLiqProd | Tick Box | QLiqProd and associated tab pages (e.g. Qm) will become visible, showing the properties of the combined feed stream. This will not include any vapours which are sent to the Tube Vap Out stream. See Material Flow Section. |
| ShowQRecirc | Tick Box | Only visible if the Recirc option has been selected. QRecirc and associated tab pages (e.g. Qm) will become visible, showing the properties of the recirculation stream. See Material Flow Section. |
| ShowQTubeIn | Tick Box | Only visible if the Recirc option has been selected. QTubeIn and associated tab pages (e.g. Qm) will become visible, showing the properties of the combined liquor feed stream including the recirculation stream. This is the sum of the LiqFeed and Recirc streams. See Material Flow Section. |
Results | ||
| U*A | Calc | heat exchanger UA. |
| LMTD | Calc | heat exchanger log mean temperature difference |
| TheoDuty | Calc | Theoretical duty of the falling film evaporator heat exchanger. The equation for this is: Q = UA * LMTD |
| MaxTheoDuty | Calc | The maximum possible theoretical duty of the falling film evaporator heat exchanger. This defines the maximum possible energy transfer that from steam at the condensing temperature to solution at the flash temperature at the tube side pressure. So, Q = UA * (Tc - Tf). This energy transfer cannot be achieved in practice, as the solution heats up and leaves the unit at a temperature greater than Tf. |
| RqdArea | Calc | The calculated area required to perform the heat exchanger duty. |
| MaxCondDuty | Calc | The maximum possible duty available from condensing the steam. |
| DutyBalance | Calc | Only visible with the Condensing Method. Difference between MaxCondDuty and TheoDuty. If this is greater than user specified tolerance ReportToleranceDuty then a warning condition message is given. |
| Recirc.Qv | Calc | Only visible if the Recirc option has been selected. The volume flow of the recirculation stream. |
| Recirc.Qm | Calc | Only visible if the Recirc option has been selected. The mass flow of the recirculation stream. |
| Tube Side | ||
| Tube.In.T | Calc | Temperature of the stream entering the Tube side. |
| Tube.Out.T | Calc | Temperature of the stream leaving the Tube side. |
| Tube.DeltaT | Calc | The difference in temperature between the stream entering the tube side and the stream leaving the tube side. |
| Tube.In.P | Calc | Pressure of the stream entering the Tube side. |
| Tube.SatP | Calc | The saturation pressure of the stream entering the Tube side. |
| Tube.Qm | Calc | Mass flow through the tube side. |
| EnthalpyIn | Calc | Enthalpy of the stream entering the Tube side. |
| EnthalpyOut | Calc | Enthalpy of the stream leaving the Tube side. |
| VapourRate | Calc | The evaporation rate. |
| Shell Side | ||
| Shell.In.T | Calc | Temperature of the stream entering the Shell side. |
| Shell.Out.T | Calc | Temperature of the stream leaving the Shell side. |
| Shell.SatT | Calc | Shell side Saturation temperature. |
| Shell.Superheat | Calc | The degree of superheat on the shell side. |
| Shell.P | Calc | Shell pressure. |
| Shell.Qm | Calc | The mass flowrate going through the Shell side. |
| CondRate | Calc | The condensate rate. |
| CondDemand | Calc | The condensate demand. |
| DeltaH | Calc | The change of enthalpy on the Shell side. |
| SpecVapLoad | Calc | The specific vapour load (flow of vapour per unit area). |
Adding this Model to a Project
Insert into Configuration file
Sort either by DLL or Group.
|
|
DLL: |
SugarUnits.dll |
→ |
Units/Links |
→ |
Sugar: Falling Film Evaporator(3) |
|
or |
Group: |
Energy Transfer |
→ |
Units/Links |
→ |
Sugar: Falling Film Evaporator(3) |
See Project Configuration for more information on adding models to the configuration file.
Insert into Project
|
|
Insert Unit |
→ |
Sugar |
→ |
Falling Film Evaporator(3) |
See Insert Unit for general information on inserting units.
Hints and Comments
- Currently, the Falling Film Evaporator is NOT included in the groups of models that will form a Flash Train. Therefore, if a Flash tank and Falling film evaporator is placed together, it will NOT automatically demand steam from the flash tank. Thus, the user needs to configure the flash tank as if it is stand-alone, then the steam evaporated can be used to feed the Falling film evaporator.
- If the FFE is reporting mass balance errors, check the following:
- When OpMode is Live Steam and DemandMode is selected, then is the Steam flow rate being controlled and reached target VapourFlow.Reqd?
- Is the Heat Transfer Area large enough to condense all the steam input?
- Is there reasonable delta T between Liquor and Steam inputs?
- Is MaxCondDuty = TheoryDuty? If not, use a PID controller to adjust Pout to get the correct values. If this does not work, need to recheck Heat Transfer Area.
- Is the Steam Feed reasonable and/or controlled correctly?
- The reporting tolerance (by default this is a hidden field) may be too tight, perhaps reduce this.
- The Steam feed (Shell In) should be 100% H2O(g). The inclusion of other vapours or phases is not supported.
- The Tube In should not include any vapours.
Duty Balance
- For general models, you will need to control the FFE model in some way to achieve Duty Balance. How this control is done depends on the overall configuration. There are three key model parameters:
- Heater Area.
- Flash Pressure.
- Heat Transfer Coefficient.
- In a Rating calculation, you are given the Area and the Heat Transfer Coefficient. Adjust the pressure to get Duty Balance.
- In a Design calculation, you know the required pressures, and HTC, so adjust the area to get balance
- In Plant Tuning, you know the pressures (from plant data) and areas (as built), but the heat transfer coefficients will have changed because of scaling and fouling. Adjust the HTC.
Set up a PID controller to adjust the appropriate parameter such that the Duty Balance is zero.
Recirculation
In practice, Falling Film Evaporators are operated with a large fraction of the product recirculated to the inlet. This has two key effects:
- Since the product liquor is cold, and a large fraction is mixed with the incoming liquor, it is possible for the incoming liquor to be hotter than the vapour temperature. Without recirculation, there could be no heat transfer since the vapour would not condense.
- Recirculation increases the tube side heat transfer coefficient since velocities are higher.
With inadequate recirculation, the liquor temperature may still be higher than the steam temperature and the unit will not operate. If you get an error message (Incoming Liquor Temperature Higher than Steam Temperature) increase the recirculation.