Compressor

Navigation: Models ➔ Pressure Changing Models ➔ Compressor

---

General Description

The compressor model can be used to increase the pressure of streams which consist mostly of gases. The user will receive a warning if the fraction of vapours in the feed is less than 99%.

• The model can also be used as a Reducer or expander, reducing the pressure isentropically, and allowing recovery of work.

The compressor model can be inserted in a steam line that is part of a Flash Train.

Diagram

The diagram shows the default drawing of the Compressor, with the required connecting streams. The unit will not operate unless all of the above streams are connected.

The physical location of the connections is not important, the user may connect the streams to any position on the drawing.

Inputs and Outputs

Label	Required Optional	Input Output	Number of Connections		Description
			Min	Max
Input	Required	In	1	1	Input stream to compressor.
Output	Required	Out	1	1	Output stream from compressor.

Behaviour when Model is OFF

If the user disables the unit, by un-ticking the On tick box, then the material will flow straight through the Compressor with NO change to either Temperature or Pressure.

So basically, the unit will be 'bypassed' without the user having to change any connections.

Model Theory

Mass and Energy Flows

Equations

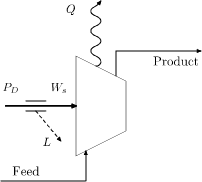
The overall energy balance for a compressor is given by

[math]\displaystyle{ W - Q = H_o - H_i }[/math]

Here [math]\displaystyle{ W }[/math] is the shaft work, [math]\displaystyle{ Q }[/math] is heat flow, [math]\displaystyle{ H_i }[/math] is the total feed enthalpy (kW), and [math]\displaystyle{ H_o }[/math] is the product enthalpy.

The required drive power input is [math]\displaystyle{ P_D = W + L }[/math], where [math]\displaystyle{ L }[/math] is the power loss in the drive train, bearings and other mechanical components.

• Some care is needed with sign conventions here. Similar equations apply for both turbines and compressors, and [math]\displaystyle{ W }[/math] may refer to either work input (as in a compressor) or work output (for a turbine or combustion engine).

The isentropic methods assume the process is adiabatic; there are no heat flows in or out of the compressor, so [math]\displaystyle{ Q = 0 }[/math]. Polytropic methods allow for heat flow into or out of the compression process. If the adiabatic efficiency is not 100%, then the process is not truly isentropic - there is a subsequent correction to the final stream enthalpy where some mechanical input work increases the temperature of the product stream (hence a net gain in entropy)

In all the subsequent discussion a subscript "i" (in) refers to feed (e.g. [math]\displaystyle{ T_i }[/math] for inlet temperature) and a subscript "o" (out) is for product conditions.

Isentropic Method (Ideal Gas Calcuations)

For an ideal gas:

[math]\displaystyle{ C_p = C_v + R }[/math]

where:

[math]\displaystyle{ C_p }[/math] = molar heat capacity at constant pressure.

[math]\displaystyle{ C_v }[/math] = molar heat capacity at constant volume.

[math]\displaystyle{ R }[/math] = universal gas constant

The k value, the ratio of specific heats, can be calculated as follows:

[math]\displaystyle{ k = \cfrac{C_p}{C_p - R} }[/math]

For an ideal gas with constant heat capacities, which undergoes a mechanically reversible, adiabatic (or isentropic) process, the following equation applies:

[math]\displaystyle{ \cfrac{T_o}{T_i}=\left (\cfrac{P_o}{P_i}\right)^{1-1/k} }[/math]

This can be rewritten as:

[math]\displaystyle{ T_{o} = T_{i} \times \left (\cfrac{P_{o}}{P_{i}}\right)^{1-1/k} }[/math]

where:

[math]\displaystyle{ T_{o} }[/math] = outlet temperature

[math]\displaystyle{ P_{o} }[/math] = outlet pressure

[math]\displaystyle{ P_{i} }[/math] = inlet pressure

[math]\displaystyle{ T_{i} }[/math] = inlet temperature

Isentropic Full Method (Real Gas Calculations)

For situations where Cp is not constant through the compression process, the isentropic full method may be used. This method assumes that compression process is isentropic (mechanically reversible and adiabatic) so that the entropy of the gas is constant throughout the process (the same as above), [math]\displaystyle{ S_{o} = S_{i} }[/math]. However, the final temperature is found by solving for a temperature where the entropy of the outlet stream at the outlet pressure matches the entropy of the inlet stream. This method is more accurate than the isentropic method above (which assumes an ideal gas with constant specific heat).

The isentropic full method should be used for compression of steam and other vapors which have nonideal behaviour.

Isentropic Efficiency and Work

Given the inlet temperature and pressure and the outlet pressure, the outlet temperature can be calculated. The outlet temperature and pressure can be used to find the outlet enthalpy, [math]\displaystyle{ H_{out} }[/math]. The work required will be the enthalpy difference of the gas between the inlet and the outlet of the compressor. For a reversible, adiabatic process, this will be the minimum or ideal amount of work required for compression:

[math]\displaystyle{ W_{s} = {H_{o}}-{H_{i}} }[/math]

The adiabatic efficiency [math]\displaystyle{ \eta_A }[/math] is used for the Isentropic and isentropic full methods and is defined as:

[math]\displaystyle{ \eta_A=\cfrac{{{W}_{s}}}{{{W}_{a}}} }[/math]

where:

[math]\displaystyle{ W_{s} }[/math] = isentropic or ideal work

[math]\displaystyle{ W_{a} }[/math] = actual work required

The actual work includes fluid friction and other irreversible losses. When the efficiency is less than 100%, the final enthalpy is found by calculating the isentropic work, dividing it by the efficiency and adding it to the inlet enthalpy. This gives the outlet enthalpy. A temperature is then found that matches the outlet enthalpy at the given outlet pressure.

Polytropic Compression

For a polytropic process, there is additional heat flow in or out. (The polytropic or "small Stage" efficiency is sometimes used to compare the performance of compressors with multiple stages, with interstage cooling)

Polytropic Method (Deprecated)

• This method uses the same efficiency calculation and parameters as the Isentropic methods. It will be removed in future releases.

Polytropic Method with Heat Flow

The calculations here are only rigorous for ideal gases with constant specific heat; results should otherwise be used as indicative quantities only. For example, the model may show heat flows for adiabatic conditions when used with gases with non-constant specific heat.

The polytropic efficiency [math]\displaystyle{ \eta_p }[/math] is used as follows:

[math]\displaystyle{ N = \cfrac{n-1}{n} = \frac1{\eta_p}\cfrac{k-1}{k} }[/math]

then

[math]\displaystyle{ T_{o} = T_{i} \times \left (\cfrac{P_{o}}{P_{i}}\right)^N }[/math]

When the polytropic efficiency is 100%, the polytropic method is equivalent to the isentropic method. As with the isentropic method, once the outlet temperature has been determined for the outlet pressure, then the outlet enthalpy can be found directly.

• The polytropic efficiency is applied to the exponent in the temperature equation
• If the value is <1, the exponent is greater than the isentropic exponent, so the temperature rise is higher; this requires a net inflow of heat [math]\displaystyle{ Q \gt 0 }[/math]
• If the value is >1, the temperature rise is lower than the isentropic case, so there is a net outflow of heat. For large values of [math]\displaystyle{ \eta_p, \, N\rightarrow 0 }[/math], so there is no temperature change (isothermal compression)

NB the polytropic efficiency is not equal to the adiabatic efficiency (except when the pressure ratio is one, i.e. zero pressure rise). For a given polytropic efficiency, the adiabatic efficiency will vary as a function of pressure ratio and decrease as the pressure ratio increases.

Compressor Power

For all methods the compressor shaft power [math]\displaystyle{ W_S }[/math] is the enthalpy change between the inlet and outlet, plus heat flow:

[math]\displaystyle{ W_S = H_{o}-H_{i} + Q }[/math]

For isentropic processes, the heat flow is zero, so we can directly determine the shaft power from the enthalpy change.

For Polytropic processes, we cannot derive the power directly from the change in enthalpy since we need to know the heat flow as well. (In the case of an isothermal process, the feed and product enthalpies are equal for an ideal gas, but we still need compressor power; some of which becomes heat outflow.)

If n>1

[math]\displaystyle{ W_S = \frac n{n-1}\left(p_o V_o - p_i V_i\right)\qquad }[/math] where [math]\displaystyle{ V }[/math] is the volume flow

If n=1 (isothermal compression)

[math]\displaystyle{ W_S = p_i V_i \ln p_i/p_o }[/math]

The actual drive power [math]\displaystyle{ P_D }[/math] required to run the compressor includes the mechanical drive efficiency [math]\displaystyle{ \eta_m }[/math] to account for the efficiency of the motor, gearbox, belts, etc.

[math]\displaystyle{ P_D = W_S/\eta_m }[/math]

To understand the application of polytropic compression, consider the case when [math]\displaystyle{ n=1 }[/math] so that the temperature exponent N=0 and there is no temperature increase between the feed and product. Since the feed and product streams have the same temperature (hence for an ideal gas the same enthalpy) we then have a heat flow out of the compressor equal to the shaft work. As n increases, the heat flow decreases, while the temperature of the product increases. For the isentropic case the heat flow is zero, and the enthalpy difference between product and feed is equal to the shaft work. For n greater than the isentropic value, the enthalpy difference is greater than the shaft work, and we require a heat inflow into the model.

Calculation Steps

Step 1) Determine the outlet pressure based on user specified value, boost or ratio.

Step 2) Select the calculation method.

Step 2) If the user has specified a value for k, use this value in the calculations, otherwise calculate k as the ratio of Cp to Cv.

Step 3) Calculate the outlet temperature based on the selected method and efficiencies.

Step 4) Calculate the outlet enthalpy based on the outlet temperature and pressure.

Step 5) Calculate the Compressor Power and the drive power required

Assumptions, Limitations and comments

1. Depending on method selected, this model assumes ideal gas behaviour and/or correct thermodynamic data for the gas species present.
2. There are no chemical reactions or phase change occurring during compression.
3. The isentropic and polytropic methods allow user entry of the specific heat ratio, k, which will override the calculated value. This may be used to approximate compression where there is significant heat transfer during the process.
4. The feed stream should contain only gases. Small amounts of liquids and solids will have little affect. The outlet temperature and pressure are determined by the gases present in the stream only. Any liquids or solids in the inlet will be assumed to exit the compressor at this new temperature and pressure. When the power is calculated using the enthalpy difference between the inlet and outlet, this will include any solids or liquids in the stream. Thus the presence of solids and liquids will usually lead to an increase in power requirements.
5. The model can also be used as a pressure reducer or expander. Set the pressure ratio to a value less than 1, or a negative pressure boost. The compressor power will also be negative (which is the work that can be recovered by expanding the stream isentropically)
6. Note: If the stream contains no gases, then the model will produce unrealistic results.

References

1. Bloch H.P. A Practical guide to Compressor Technology, McGraw-Hill 1996

2. Perry et al Perry's Chemical Engineers' Handbook 6^th Edition, McGraw-Hill 1984

Data Sections

Summary of Data Sections

1. Compressor tab - contains the main configuration information relating to the unit.
2. QFeed - Available from Build 139. Optional tab, visible if ShowQFeed is enabled. This and subsequent tab pages, e.g. QFeed.. and Sp, shows the properties of the feed stream. The tags in the QFeed tab are valid even when the ShowQFeed option is not selected.
3. QProd - Available from Build 139. Optional tab, visible if ShowQProd is enabled. This and subsequent tab pages, e.g. QProd.. and Sp, shows the properties of the product stream. The tags in the QProd tab are valid even when the ShowQProd option is not selected.
4. Info tab - contains general settings for the unit and allows the user to include documentation about the unit and create Hyperlinks to external documents.
5. Links tab, contains a summary table for all the input and output streams.
6. Audit tab - contains summary information required for Mass and Energy balance. See Model Examples for enthalpy calculation Examples.

Compressor Page

Unit Type: Compressor - The first tab page in the access window will have this name.

Tag (Long/Short)	Input / Calc	Description/Calculated Variables / Options
Tag	Display	This name tag may be modified with the change tag option.
Condition	Display	OK if no errors/warnings, otherwise lists errors/warnings.
ConditionCount	Display	The current number of errors/warnings. If condition is OK, returns 0.
GeneralDescription / GenDesc	Display	This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here. If this field is blank, then SysCAD will display the UnitType or SubClass.
Requirements
On	Tickbox	If the unit is disabled, by un-ticking this box, then material flows straight through the unit, with no change to temperature or pressure.
PressMethod	Fixed	The user specifies the outlet pressure from the Compressor.
	Boost	The user specifies the pressure boost of the compressor.
	Ratio	The user specifies the ratio of the outlet pressure to the inlet pressure.
PressureReqd / P_Reqd	Input	Only visible if Fixed is chosen for the Pressure method. This sets the required pressure of the outlet (discharge) stream.
PressBoostReqd / PBoostReqd	Input	Only visible if Boost is chosen for the Pressure method. The difference in pressure between the inlet and outlet streams.
PressRatioReqd / PRatioReqd	Input	Only visible if Ratio is chosen for the Pressure method. The ratio of the outlet pressure to the inlet pressure.
MaxPressRatio / MaxPRatio	Input	The maximum compression ratio that the Compressor can provide. If the required final pressure / inlet pressure > than this value, then SysCAD will restrict the final pressure so that the maximum pressure ratio is not exceeded. The unit will give the user an error message if this occurs.
CalculationMethod / Method	Isentropic / Isentropic(IdealGas)	The isentropic outlet temperature will be calculated using the pressure ratio, inlet temperature and the ratio of heat capacities (k).
	Isentropic Full / Isentropic(RealGas)	The outlet temperature will be calculated using the pressure ratio and finding an outlet temperature such that the outlet entropy at the outlet pressure matches the inlet entropy.
	Polytropic	The outlet temperature will be calculated using the pressure ratio, inlet temperature, ratio of heat capacities (K) and the polytropic efficiency. Deprecated; will be removed
	Polytropic(IdealGas)	Available from Build 139.32609. Polytropic Method.
SpecifyK	Tickbox	This allows the user to specify the heat capacity ratio,k. If this is left unchecked, then the model will assume ideality and use equation (1) to calculate k based on Cp values in the species database.
k	Input	Only visible if SpecifyK option is selected. This is the user specified value of k, the ratio of specific heats of the gas in the feed stream.
OldAdiabaticEffCalc	Input	This original calculation is inaccurate for real gases such as steam and this will be removed. If you have this enabled and see warning messages, disable it: some retuning of the model will be needed Deprecated; will be removed in 140
Adiabatic.Efficiency / AdiabaticEff	Input	Only visible if one of the Isentropic methods are chosen for the Calculation method. This efficiency is used to calculate the actual work required from the isentropic work. A lower efficiency will increase the work required.
Polytropic.Efficiency / PolytropicEff	Input	Only visible if Polytropic is chosen for the Calculation method. This is the ratio of shaft power to enthalpy gain in the compressed gas, and may be greater than 1.
Compressor.Efficiency / CompressorEff	Input	This is the mechanical efficiency of the compressor drive and gear box (if present) and is used to calculate the drive motor power required from the IdealPower. A lower efficiency will lead to a larger Power and a larger difference between Power and IdealPower.
Options
ShowQFeed	Tickbox	Available from Build 139. When selected, the QFeed and associated tab pages (e.g. Sp) will become visible, showing the properties of the feed stream. See Material Flow Section. Tags in the QFeed tab can be used for controllers (e.g.: PGM files) and reports even when this option is not selected.
ShowQProd	Tickbox	Available from Build 139. When selected, the QProd and associated tab pages (e.g. Sp) will become visible, showing the properties of the product stream. See Material Flow Section. Tags in the QProd tab can be used for controllers (e.g.: PGM files) and reports even when this option is not selected.
Results
MassFlow / Qm	Calc	The total mass of material flowing through the compressor.
TemperatureIn / Ti	Calc	The temperature of material at the inlet of the compressor.
TemperatureOut / To	Calc	The temperature of material at the outlet of the compressor.
PressureIn / Pi	Calc	The actual pressure at the inlet of the compressor.
PressChange / dP	Calc	The pressure change in the compressor.
PressureOut / Po	Calc	The actual pressure at the outlet of the compressor.
PressRatio / PRatio	Calc	The pressure ratio of the compressor = Pressure Out / Pressure In.
DensityIn / Rhoi	Calc	The density of material at the inlet of the compressor.
DensityOut / Rhoo	Calc	The density of material at the outlet of the compressor.
VapourFracIn / Vfi	Calc	Vapour Mass Fraction at the inlet of the compressor.
VapourFracOut / Vfo	Calc	Vapour Mass Fraction at the outlet of the compressor.
Energy Balance
MaxEffPower	Calc	Available from Build 139.32609. This is the IdealPower at Polytropic or Adiabatic efficiency of 1 (100%).
IdealPower	Calc	This is the amount of power put into the fluid being compressed and is the enthalpy difference between the inlet and outlet streams per unit time. The lower the efficiency the more power required to achieve the same pressure.
Isothermal.Power	Calc	Available from Build 139.32609. Compression work under isothermal conditions.
Power	Calc	The required compressor drive power for the given adiabatic and drive efficiencies.
HeatTransfer	Calc	This field is only visible if the Polytropic (IdealGas) Method is selected. This is Q which is equal to MaxEffPower - HeatFlow.
HeatFlow	Calc	Available from Build 139.32609. The energy balance heat flow for the model. This is equal to the enthalpy difference between the inlet and outlet streams, which is also equal to the reported IdealPower.
Gas.MWT	Calc	The weighted average of the molecular weights of the vapours in the inlet stream.
Gas.Cp	Calc	The weighted average of the heat capacities at constant pressure (Cp) of the vapours in the inlet stream.
Gas.Cv	Calc	The heat capacity at constant volume (Cv) of the vapours in the inlet stream. This is calculated using the heat capacity at constant pressure (Cp).
Gas.K	Calc	The ratio of the Gas Cp to the Gas Cv, i.e. the K value. A postscript description is given if the selected Method uses this value of K for the calculation.

Adding this Model to a Project

Add to Configuration File

Sort either by DLL or Group:

	DLL:	Piping2.dll	→	Units/Links	→	Piping: Compressor
or	Group:	General	→	Units/Links	→	Piping: Compressor

See Model Selection for more information on adding models to the configuration file.

Insert into Project Flowsheet

Insert Unit

→

Piping

→

Compressor

See Insert Unit for general information on inserting units.

Example Project

• Demo Ammonia Project
• Demo ASU WEU HBR Project