Density Correction Calculations
Navigation: Models ➔ Model Examples ➔ Density Correction Calculations
Related Links: Density, Density Calculation
This page describes how density correction calculations are performed.
Density Correction Methods
The mass fraction of a species i, (MFi), can be calculated in two separate ways. The user may define which method to use in the project using tag PlantModel.DensityCorrection - see Plant Model-Species tab page.
The user may view the density of a solution containing ONLY the solvent and a single solute (at a user defined mass fraction) on the Liquids tab page of the Species Properties access window in a project.
Fraction in Solvent Only
- Most data is obtained from single solute solutions. This method considers only the individual solute i and the solvent when calculating the MF value used in the density correction function:
Eq 1) [math]\displaystyle{ MF_i = \cfrac{Solute_i}{Solvent + Solute_i} \, }[/math]
- Notes:
- The solvent can be water or any other liquid, as selected in the Solvent section of the species database. (Please see Species Table - Density and Editing SysCAD Database)
- Since this method uses only the masses of the solvent and the individual solute, the calculated density correction factor will be Larger than the value calculated using the method below.
Fraction in Aqueous Solution
- In this case the solvent MUST be water. The Solute would be an aqueous species.
- The calculation will consider water and ALL the solvent species that use the same density correction method when calculating the MF value for i:
Eq 2) [math]\displaystyle{ MF_i = \cfrac{Solute_i}{Water + Sum(All Solvent Species)} \, }[/math]
Notes:
- SysCAD will use water and species with a Density Correction when calculating the species mass fraction. Other species, including aqueous species that do not have a density correction are excluded from the mass fraction calculations.
- The count of Solute species is given on SDB - FS SDB tab page and on the SDB - Liquids tab page you can see the species with density corrections based on the AppDens column
- Since this method uses the mass of water and the masses of all of solute species, the calculated density correction factor will be Smaller than the value calculated using the first method, and hence the solution density will be lower.
Implementation of the Density correction Function
1. The density correction factor [math]\displaystyle{ D_i }[/math] for each solute is calculated as follows:
Eq 3) [math]\displaystyle{ \qquad D_i = F_i(MF_i) - F_i(0) \, }[/math]
- where [math]\displaystyle{ F_i(MF_i) }[/math] finds the density correction value at the Mass Fraction [math]\displaystyle{ MF }[/math] of i in the stream. The method used to calculate [math]\displaystyle{ MF_i }[/math] depends on if Eq1 or Eq2 DenesityMethod is used.
- [math]\displaystyle{ F_i(0) }[/math] is the density correction value at the Mass Fraction of 0.
Notes:
- The result of this is that the first term a in the Poly(a, b, c, d...) function has no effect.
- Please see Density Correction for details of this function.
- The density correction factor used for each species is reported in streams as described in Material Flow - Density Correction.
2. The individual solute factors are then summed and multiplied by the Pure Solvent Density [math]\displaystyle{ \rho_P }[/math] to determine the adjusted density of the solutes in solution:
Eq 4) [math]\displaystyle{ \qquad\rho_S = \rho_P \times \left( 1 + \sum D_i \right) \, }[/math]
- The pure solvent density is at stream temperature and pressure.
- The density of the pure solvent may also be a function of temperature. In which case the density of the solvent at the relevant temperature is first calculated and then this value is multiplied by the solute correction factor.
- Normally the solvent is water, so the density for water that is used will be at stream temperature and pressure.
- The density correction function itself is independent of temperature and pressure.
Notes:
- The overall density correction (tag Solvent.CorrFactor), pure solvent density (tag Solvent.Rho) and the resulting "apparent" density (tag Solvent.AppRho) of the solutes with solvent are all reported in streams as described in Material Flow - Density Correction.
Example Solution Density Calculations
For analysis, additional information for density calculations can be reported. To view these the "DensityCorrection" option must be selected for Include Properties. This global setting can be selected with "Include Properties" button at top of any stream page (e.g. Qo, QFeed) or in Plant Model-Views tab page.
EXAMPLE 1
Consider the following example at a temperature of 25°C and 1 atmosphere.
| Compound | Mass (kg) |
Density of Compound at (100wt%) (kg/m³) |
Density of compound contribution using Mass Weighted Mean i.e. NO density correction (kg/m³) |
|---|---|---|---|
| H2O(l) | 88.3 | 997.05 | 880.39 |
| CuSO4(aq) | 6.1 | 3606 | 219.97 |
| NaCl(aq) | 2.4 | 2165 | 51.96 |
| CaSO4(aq) | 3.2 | 2960 | 94.72 |
| Density of mixture using Mass Weighted Mean | 1247.04 | ||
The density correction functions have the following form:
[math]\displaystyle{ F_i(x)=a+bx+cx^2+dx^3+ex^4 }[/math] (5)
- Please see Density Correction for further help on the density correction function.
Density correction functions for CuSO4(aq) and NaCl(aq) are:
[math]\displaystyle{ F = 0.9997 + 0.9173x + 2.5987x^2 - 13.708x^3 + 35.212x^4\qquad }[/math] CuSO4 (6)
[math]\displaystyle{ F = 0.9982 + 0.7085x + 0.1214x^2 + 0.3702x^3\qquad }[/math] NaCl (7)
- Here x is the mass fraction of the solute species of interest in solution.
- (Ref: Lide D.R. Handbook of Chemistry and Physics 74th Edition CRC Press)
Liquid Density:
Eq 8) [math]\displaystyle{ Liquid Density = \cfrac{Total Liquid Mass}{\cfrac{Total Liquid Mass With Density Correction} {Adjusted Density} + \big( \sum{\cfrac{Mass_i With No Density Correction} {Density_i} } \big)} \, }[/math]
CuSO4(aq) and NaCl(aq) are included with TotalLiquidMassWithDensityCorrection. CaSO4(aq) is included with sum of MassWithNoDensityCorrection.
We will calculate the density of solution using the two available methods:
| Description | Fraction in Solvent Only | Fraction in Aqueous Solution |
| Mass Fraction of H2O(l) | NA | 0.91219 (Equation 2) |
| Mass Fraction of CuSO4(aq) | 0.06462 (Equation 1) | 0.06302 (Equation 2) |
| Mass Fraction of NaCl(aq) | 0.02646 (Equation 1) | 0.02479 (Equation 2) |
| Mass Fraction of CaSO4(aq) | NA | 0.032 |
| Density Correction Factor for CuSO4(aq) (Using Equations 3 and 6) | 0.06704 | 0.06525 |
| Density Correction Factor for NaCl(aq) (Using Equations 3 and 7) | 0.01884 | 0.01765 |
| Sum of Density Correction Factors | 0.08588 | 0.0829 |
| Solvent Adjusted Density kg/m3 (Equation 4) | 1082.675 | 1079.699 |
| Liquid Density kg/m3 (Equation 8) | 1105.103 | 1102.102 |
Density and Volume display for mixtures:
EXAMPLE 2
Consider the following example at 40 °C & atmospheric pressure; determine the volumetric flow of the stream.
To determine the stream volumetric flow of the stream, we need to first compute the corrected solution density the mixture of Water-NaCl-H2SO4.
We will use the same equations given in the previous example, as well as correction equation for H2SO4 given below:
Density of H2SO4(aq)
Eq 9) [math]\displaystyle{ H_2SO_4\ DensCorrFn=1+0.5394x+1.4827x^2-4.6384x^3+7.2207x^4-3.7737x^5 }[/math]
- Where x is the mass fraction of H2SO4(aq) in solution.
- (Ref: Lide D.R. Handbook of Chemistry and Physics 74th Edition CRC Press)
Basis: 1000 kg/h
| Component | Mass Fraction | Density (kg/m3) |
Density Correction | Individual Volume Display (m3/h) |
| NaCl(aq) | 0.0900 | * | (Equation 6) 0.0800 | * |
| H2SO4(aq) | 0.0900 | * | (Equation 9) 0.0832 | * |
| H20 | 0.6300 | 992.216 | 0.6349 | |
| CuO(s) | 0.0550 | 6450 | 0.0085 | |
| Cu(s) | 0.0450 | 8920 | 0.0050 | |
| MgCO3(aq) | 0.0450 | 1000 | 0.045 | |
| CuSO4(aq) | 0.0450 | 1000 | 0.045 |
| [math]\displaystyle{ \mathbf{\mathit{Density \ solution}} }[/math] | [math]\displaystyle{ \mathbf{\mathit{= Density_{ Water \ at \ 40^{\circ}\ C} * (1 + \sum density \ correction)}} }[/math] |
| [math]\displaystyle{ = 992.216 \times (1 + 0.08 + 0.0832) = 1154.15 \mathrm{kg/m^3} }[/math] |
| [math]\displaystyle{ Liquid \ Density }[/math] | [math]\displaystyle{ = (90+90+630+45+45) / [ (90+90+630)/1154.15 + 45/1000 + 45/1000 ] }[/math] |
| [math]\displaystyle{ = 1136.63 \mathrm{kg/m^3} }[/math] | |
| [math]\displaystyle{ Liquid \ Vol \ Flow }[/math] | [math]\displaystyle{ = 900/1136.63 = 0.7918 \mathrm{m^3/h} }[/math] |
| [math]\displaystyle{ \mathbf{\mathit{Solids \ Density}} }[/math] | [math]\displaystyle{ \mathbf{\mathit{= 100 / (55/6450 + 45/8920) = 7368.12 kg/m^3}} }[/math] |
| [math]\displaystyle{ \mathbf{\mathit{Solids \ Vol \ Flow}} }[/math] | [math]\displaystyle{ \mathbf{\mathit{= 100/7368.12 = 0.01357 m^3/h}} }[/math] |
| [math]\displaystyle{ \mathbf{\mathit{Stream \ Volume}} }[/math] | [math]\displaystyle{ \mathbf{\mathit{= 0.7918 + 0.01357 = 0.80537 m^3}} }[/math] |
| [math]\displaystyle{ \mathbf{\mathit{Stream \ Density}} }[/math] | [math]\displaystyle{ \mathbf{\mathit{= 1000 / 0.80537 = 1241.67 kg/m^3}} }[/math] |
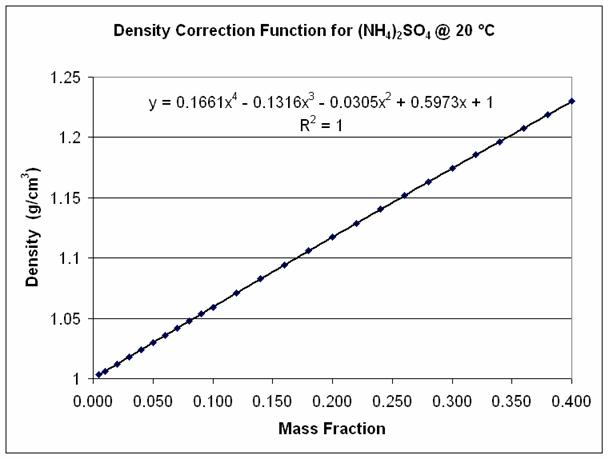
Density Correction for Solutions & Data Fitting
Given the following data for (NH4)2SO4 @ 20°C (Source: CRC Handbook of Chemistry and Physics, 60th Edition), data fitting gives the following:
| MF | Density (g/cm³) | MF | Density (g/cm³) | MF | Density (g/cm³) | MF | Density (g/cm³) | MF | Density (g/cm³) | MF | Density (g/cm³) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.005 | 1.003 | 0.05 | 1.0297 | 0.1 | 1.0593 | 0.2 | 1.1174 | 0.3 | 1.1742 | 0.4 | 1.2298 |
| 0.01 | 1.0059 | 0.06 | 1.0356 | 0.12 | 1.071 | 0.22 | 1.1289 | 0.32 | 1.1854 | ||
| 0.02 | 1.0119 | 0.07 | 1.0416 | 0.14 | 1.0827 | 0.24 | 1.1403 | 0.34 | 1.1966 | ||
| 0.03 | 1.0178 | 0.08 | 1.0475 | 0.16 | 1.0943 | 0.26 | 1.1516 | 0.36 | 1.2077 | ||
| 0.04 | 1.0238 | 0.09 | 1.0534 | 0.18 | 1.1059 | 0.28 | 1.1629 | 0.38 | 1.2188 |
Thus, density correction equation used in SysCAD is Correction : H2O(l) : Poly_MF(1.0, 0.5973, -0.0305, -0.1316, 0.1661) : Limit(0.4, 1769, On). See Density Correction.