Discussion: K Values in Multicomponent VLE

This is a Discussion Page with supplementary user information. It is not part of the core SysCAD Help Documentation - please refer to the User Guide for full documentation links.

Navigation: Product Blog ➔ Discussion Pages ➔ K Values in Multicomponent VLE

Related Links: Multiple Component VLE, Vapour Pressure (Vp), Absorption Tower (MultiK) Example Project

---

Introduction

Vapour Liquid Equilibrium (VLE) is a very useful feature in SysCAD that is covered early in the introductory tutorial. There we enable VLE in a Tank model representing an Autoclave to condense steam in the feed and heat the tank. VLE is simply a specialised form of reaction (in fact in early versions of SysCAD there was no VLE option, so if you wanted to condense steam you had to include the reaction H2O(g) -> H2O(l)). This is a common case of single component VLE where the only component is H₂O, either as liquid or vapour.

Of course it is also possible to chose a different component if other volatile species are present. When SysCAD opens a project, it looks for all species that have both vapour and liquid phases present, and these become options for the single-component VLE species. You can then chose any of them in a dropdown list on the VLE tab:

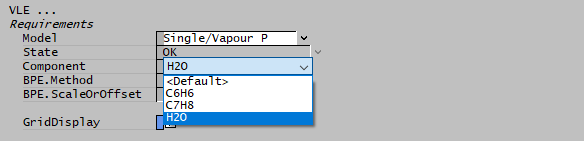
Single-component VLE works through a vapour pressure equation, which for water is the saturation curve built into IF97. To use components other than water, you must to have a vapour pressure equation specified in the species database (SDB). SysCAD can then use this, together with enthalpy calculations, to model everything from simple evaporation/condensation to complex flash trains.

Multicomponent VLE

In many situations there are several volatile components which may exist either in the liquid or vapour phase. With multiple components, there is no such thing as a boiling point for the system; instead there is a bubble point below which all components are liquid, and a dew point above which all components are vapour. The term "dew point" comes from the observation that as the temperature drops on a humid night, moisture will start to appear at some point. This temperature is far lower than the actual boiling point of water at ~100 °C, but is related to the vapour pressure of water vapour at this lower temperature - i.e. the partial pressure of moisture in the air.

The K-values used to describe multicomponent VLE also apply in the case of a single component, and we can use the condensation of water from air to illustrate this. On a hot summer night, the temperature drops to 25 °C and we observe that moisture starts to condense. At 25 °C, the vapour pressure of water is 3.17 kPa, and since we are at the dew point we know that this must also be the partial pressure of water vapour in the air. The partial pressure of an ideal gas in a mixture is also the mole fraction of the gas in the mixture, so (assuming normal atmospheric pressure) the atmospheric moisture fraction must be 3.17/101.325 = 0.0313 or 3.13% on a molar basis.

The standard notation (when discussing VLE) for the molar fraction of a component in a vapour is [math]\displaystyle{ y }[/math], and if there are multiple components, this is indexed [math]\displaystyle{ y_i }[/math]. So for our simple air-water system, the vapour fractions are (3.13%, 96.87%) where 96.87% is the air fraction (representing air as a single non-condensable species in this situation). For the liquid phase, we only have a single component which is 100% water (since the remaining air is non-condensable), and again the standard terminology is to use [math]\displaystyle{ x }[/math] or [math]\displaystyle{ x_i }[/math] as the mole fractions of species in the liquid phase.

The K-value for a component in a vapour-liquid mixture is just the ratio of the mole fraction of a component in the vapour to that in the liquid. i.e.:

[math]\displaystyle{ K = y/x }[/math] or [math]\displaystyle{ K_i = y_i/x_i }[/math] when multiple components are present

again where:

[math]\displaystyle{ y }[/math] or [math]\displaystyle{ y_i }[/math] is the component fraction(s) in the gas phase

[math]\displaystyle{ x }[/math] or [math]\displaystyle{ x_i }[/math] is the component fraction(s) in the liquid phase

For our simple water-air system, we have a K-value for water of 0.0313 which represents two things:

1. The ratio of the vapour pressure of water at 25 °C to atmospheric pressure (and thus the molar fraction for an ideal gas mixture).
2. The ratio of the molar fraction of water vapour in the air to the molar fraction of water in the liquid.

This same correspondence is also true for multicomponent systems. If we know the vapour pressures of each component at a particular temperature (calculated from their individual vapour pressure curves), we can calculate the K-values for each component. Again this is simply the ratio of the vapour pressure to the total pressure, which determines a relationship between the composition of the liquid and vapour phases of the mixture.

In summary:

• The K-values represent a compositional relationship between the gas and liquid phases.
• For ideal systems, the K-values can be calculated from the vapour pressure curve of each component.
• Given a feed composition, with a total quantity of each component specified (both liquid and vapour), we can calculate a product composition.
• We can also determine an enthalpy change between the feed and product.

Multi/Ideal K's

The Multi/Ideal K's option in the VLE sub-model implements precisely this as a flash calculation. K-values strictly determine the composition of the product and this will generally be different to that of the feed. As SysCAD is calculating the VLE, it will adjust the temperature of the product such that the enthalpy is equal to that of the feed. In doing so, the K-values will be updated (since the vapour pressures will change with temperature). As such, this is an iterative calculation. Below is a simple example with a feed of benzene (C₆H₆) and toluene (C₇H₈) liquids at a temperature higher than the bubble point. Some of the liquid is flashed to produce a product at a lower temperature.

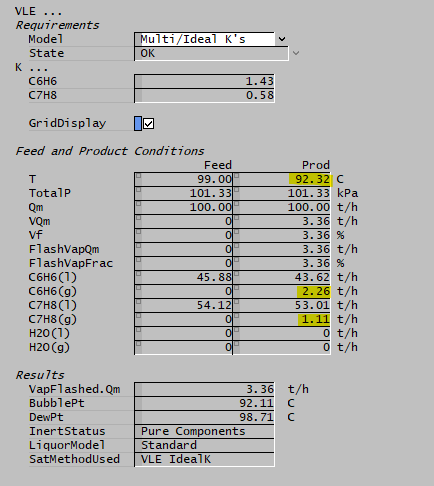
K-values represent relative volatility and indicate the tendency of a species to favour the vapour phase.

[math]\displaystyle{ K \gt 1 }[/math] : Species have a higher concentration in the vapour phase. (Non-condensable species have an infinitely large K-value.)

[math]\displaystyle{ K \lt 1 }[/math] : Species have a higher concentration in the liquid phase. (Non-volatile species have a K-value of zero.)

Note above that benzene has a higher K-value, so more is flashed to the vapour phase.

The K-values are also used to estimate the bubble and dew points of a mixture. We know that the total mole fraction of all components in the vapour [math]\displaystyle{ \sum y_i }[/math] must equal 1. If all K-values are less than 1 then the equality [math]\displaystyle{ \sum y_i = \sum K_i x_i }[/math] is unsolvable (unless non-condensable vapours are also present). As such, we can only have liquids and are below the bubble point of the mixture. Similarly if all K-values are greater than 1 we can only have vapour components and must be above the dew point.

Inert Components

Both the liquid and vapour phases in the feed may contain inert components (non-condensable or non-volatile species), for example the nitrogen and oxygen in air may be considered inert when looking at an air-water system. Aqueous components in the liquid phase may also be considered to be inert. Such components don't participate in VLE, but they do influence the mole fraction of the VLE species in the calculation. In the simple water vapour example, we need to account for the presence of the inert air in calculating [math]\displaystyle{ y }[/math] for water vapour. In some ways, inerts simplify the analysis: having inert air present guarantees that there will be some fraction of water vapour present, and we only have the dew point to consider, above which liquid water disappears altogether.

Let us look at the case of a single component, say water vapour, when [math]\displaystyle{ K = 1 }[/math]. If there are no other species (inert or otherwise) involved, the liquid and vapour are pure water and steam. In each phase the fraction of H₂O is 100%, so [math]\displaystyle{ K = 1 }[/math] no matter how the steam and water are distributed. As such, a K-value of 1 tells us nothing about how much steam and water are present, just that both are there, and we need further information (such as total enthalpy) to determine the actual composition.

Suppose now we have a feed consisting of 100 kmol/h of liquid, of which is 75% water and 25% inert liquid (by mole fraction). We also have 100 kmol/h of inert air. Suppose we are at the required temperature such that we evaporate 60 kmol/h of the water as vapour. The mole fraction of water in the vapour is now y = 60/(100+60) = 37.5%, while in the liquid it is x = (75-60)/(100-60) = 37.5% so our K-value is 1. In this case, [math]\displaystyle{ K = 1 }[/math] represents a specific composition for the system since inert components are present.

If we only had 50 kmol/h of air and evaporated just 50 kmol/h of water for a K-value of 1 (y = 50/(50+50) = 50%, and x = (75-50)/(100-50) = 50%), while for 5 kmol/h air we would have an evaporation rate of 12.5 kmol/h. Conversely if the air flow is large, then we will evaporate most of the water for the same K-value.

The point of this is that the amount of evaporation is determined not only by the K-value, but also by the presence of inert components and other volatile species. As before, the K-values are an indication of relative volatility of the components, not an absolute measure on their own.

Multi/Fixed K (User Input)

Not all liquid/vapour systems are ideal, and so SysCAD allows an alternative calculation of VLE via the Multi/Fixed K option, where you can calculate K-values externally (e.g. via PGM) and write the values to the input fields for each volatile component. Note that the terminology suggesting that this is a "fixed" value is misleading - the values should still be adjusted depending on temperature, pressure and composition of the system. Simply inputting arbitrary K-values may give rise to a physically unrealistic state, for example if the feed is liquid and the K-values determine that the mixture should be mostly vapour, a large heat addition may be required to achieve the state of equilibrium.

This option is thus intended to be used in combination with other side calculations that can provide realistic values for the Fixed K entries. The Absorption Tower (MultiK) Example Project demonstrates this, calculating the K-Values for H2O, CO2, and HCl using various methods, and writing the values to the VLE block.

Relation to Gibbs Free Energy Minimisation (GFEM)

There is a close relationship between GFEM and Multicomponent VLE, since we can predict the vapour pressure curve for a pair of components using GFEM. For a given pressure, below the boiling point the liquid free energy [math]\displaystyle{ G }[/math] is lower, while above the boiling point the vapour free energy is lower. At the boiling point the two values are equal. Note the crossover point in the following diagram:

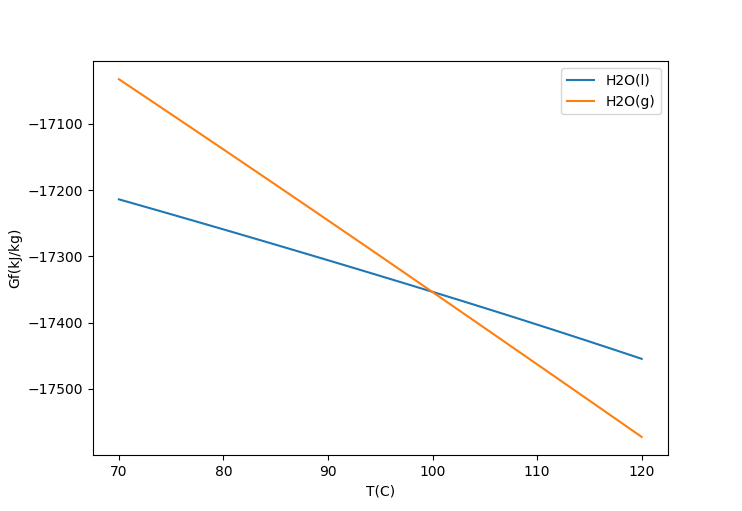
For an ideal gas:

[math]\displaystyle{ G(T, p) = G_v(T) - RT\ln p/p^0 }[/math]

where [math]\displaystyle{ p^0 }[/math] is the reference (atmospheric) pressure.

For a liquid, we assume [math]\displaystyle{ G_L(T) }[/math] is independent of pressure. At the boiling point these two quantities are equal, so:

[math]\displaystyle{ G_v(T) - RT\ln p/p^0 = G_L(T) \qquad }[/math] or [math]\displaystyle{ \qquad RT\ln p/p^0 = G_L(T)-G_v(T) = \Delta G(T) }[/math]

where [math]\displaystyle{ \Delta G(T) }[/math] is the difference between liquid and vapour free energies at reference (atmospheric) pressure.

So we can then predict vapour pressure:

[math]\displaystyle{ p = p^0\exp(-\Delta G/RT) }[/math]

This value can then be used to calculate K-values for the system.

---

First Posted: 22 September 2023

Reference Build: 139.33632

For questions or feedback, please contact us at [email protected].