Matrix Class

Navigation: PGMs ➔ Classes ➔ Matrix Class

Global Pre-Defined Class Instances			SysCAD Pre-Defined Classes
Sp Database SDB Class	Particle Size Defn PSD Class	Plant Model PM Class	Array Class	StrArray Class	Matrix Class	TagSelect Class	Time Class	Noise Class

Latest SysCAD Version: 25 October 2024 - SysCAD 9.3 Build 139.36522

Related Links: Defining a Class, Example PGM Files

Description

The MATRIX class provides member functions, to create a dynamic matrix and manipulate its elements.

The user may read in a matrix from a text file.
The user may set constant values into a matrix when it is declared.
Various Matrix Algebra functions are available.

Notes:

The initial length (rows and columns) of the matrix is zero.
The matrix is zero indexed, i.e. the index starts at zero.
If the index is out of range (0 <= index < length) then a runtime "PGM class execution error" will occur and the MATRIX operation will be ignored.
If the user reads values into a matrix from a CSV file, the file may contain alphanumeric strings, but the alphanumeric strings must NOT contain any spaces.

Data Members

None

Member Functions

The example in the table below is based on the following variables and matrix declarations.

Matrix a, b, c, L, M, M1, M2, I, Iv1, CIv1
Real   d, Qty, Det
Long   RowCount, ColCount
Bit    OK, EqualOK, MultMatrixOK, MultArrayOK, InvertOK, SolveOK
Array  TestRow, TestCol, xA, X

Note that a number of the functions below return a bit to indicate whether they have been performed successfully or not. The use of this bit is optional. For example, the statement M.Load("$Prj\MyData.txt") will read a text file of data into the matrix M. If the statement is written as OK = M.Load("$Prj\MyData.txt"), the text file will be written into M as before and the bit variable OK will be set to 1 if the operation was successful or 0 if it was not. There is usually no other message to indicate if an operation has failed.

Call	Functionality	Return Type	Parameters	Example
SetSize(Rows,Columns)	The matrix size is set to rows x columns.		Rows : the required number of rows of the matrix, is of data type LONG. Columns : the required number of columns of the matrix, is of data type LONG.	a.SetSize(5, 3)
GetRowCount()	This returns the current number of rows of the matrix.	Long	None	RowCount = a.GetRowCount()
GetColCount()	This returns the current number of columns of the matrix.	Long	None	ColCount = a.GetColCount()
Rows() Available from Build 139.30807.	This returns the current number of rows of the matrix.	Long	None	RowCount = a.Rows()
Cols() Available from Build 139.30807.	This returns the current number of columns of the matrix.	Long	None	ColCount = a.Cols()
SetIdentity(size)	The matrix is set as an identity matrix of the specified size.		size : the required number of rows/columns of the matrix, is of data type LONG. The identity matrix is a square matrix with diagonal having values of 1 and everything else zero.	I.SetIdentity(3) This will return a matrix \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
SetAll(value)	This sets all the elements of the array to the specified value.		value : the required initialising value. This is of data type REAL.	a.SetAll(0)
SetAt(Rowindex, ColumnIndex, value)	This sets the element of the matrix, which corresponds to the given indexes to the specified value.		RowIndex : the index of the required Row entry in the matrix (Note: index starts at zero). This is of data type LONG. ColumnIndex: the index of the required Column entry in the matrix (Note: index starts at zero). This is of data type LONG.	a.SetAt(2, 2, 2.2) OR a.SetAt(2, 2, ["P_001.Qm (t/h)"])
GetAt(RowIndex, ColumnIndex)	This retrieves the value of the element of the matrix, which corresponds to the given indexes.	Real	RowIndex: the index of the required Row entry in the matrix (Note: index starts at zero). This is of data type LONG. ColumnIndex: the index of the required Column entry in the matrix (Note: index starts at zero). This is of data type LONG.	d = a.GetAt(3, 1)
IncAt(RowIndex, ColumnIndex, value)	This sets the element of the matrix with the increased value.		RowIndex: the index of the required Row entry in the matrix (Note: index starts at zero). This is of data type LONG. ColumnIndex: the index of the required Column entry in the matrix (Note: index starts at zero). This is of data type LONG. value : the value to which the specified element, in the matrix, will be increased. This is of data type REAL.	a.IncAt(3, 2, Qty)
DecAt(RowIndex, ColumnIndex, value)	This sets the element of the matrix with the decreased value.		RowIndex: the index of the required Row entry in the matrix (Note: index starts at zero). This is of data type LONG. ColumnIndex: the index of the required Column entry in the matrix (Note: index starts at zero). This is of data type LONG. value : the value to which the specified element, in the matrix, will be decreased. This is of data type REAL.	a.DecAt(0, 2, Qty)
Sum()	This calculates the sum of all elements in the matrix.	Real	None	d = a.Sum()
Avg()	This calculates the average of all elements in the matrix.	Real	None	d = a.Avg()
Min()	This returns the minimum value of all elements in the matrix.	Real	None	d = a.Min()
Max()	This returns the maximum value of all elements in the matrix.	Real	None	d = a.Max()
Norm() Available from Build 139.30807.	This normalises the contents of the matrix such that the sum is 1. Equivalent to a.OpDiv(a.Sum()).		None	a.Norm()
SortByRefRow(RowIndex, Ascending) Available from Build 139.30807.	This re-arranges all the columns in the matrix in ascending / descending order based on the specified reference row. Swaps columns so that the specified row is sorted.		RowIndex: the index of the required reference Row in the matrix to determine sort sequence (Note: index starts at zero). This is of data type LONG. Ascending: 1 (true) or 0 (false) value for sorting in ascending or descending order. This is of data type bit.	a.SortByRefRow(0, true)
SortByRefCol(ColIndex, Ascending) Available from Build 139.30807.	This re-arranges all the rows in the matrix in ascending / descending order based on the specified reference column. Swaps rows so that the specified column is sorted.		ColIndex: the index of the required reference Column in the matrix to determine sort sequence (Note: index starts at zero). This is of data type LONG. Ascending: 1 (true) or 0 (false) value for sorting in ascending or descending order. This is of data type bit.	a.SortByRefCol(0, false)
Load(filename)	This creates a new matrix from a file. The first element on each line, of the specified file, is read in as an element of the matrix, until either an empty line or end-of-file character is reached. The function returns, True if the file was read or, False if the file was not read. Note: if any elements exist in the matrix, prior to calling Load, these elements will be overridden.	Bit	fileName : either the actual filename and path in quotations or a STR variable, which refers to the file. Use $Prj in the folder string for folders relative to the project folder.	OK = b.Load("$Prj\Data.txt")
Save(filename)	This saves the matrix data to a comma separated text file. If the specified file exists it is overwritten. The function returns, True if the file was saved or, False if the file was not saved. This could fail for any file access reason, for example: invalid folder, invalid filename, file access error, file already open in another application, etc.	Bit	fileName : the actual filename and path in quotations or a STR variable, which refers to the file. Optionally use $Prj in the folder string for folders relative to the project folder.	OK = a.Save("OutputData.csv")
CopyToClipboard()	This saves the array data to the clipboard. The function returns the value, True.	Bit	None	a.CopyToClipboard()
SetAll(value)	This sets all the elements of the Matrix to the specified value.		value : the required value. This is of data type REAL.	a.SetAll(0)
Scale(value)	All the elements of the Matrix are scaled by the specified value (New value = original value * Scale).		value : the required scaling factor. This is of data type REAL.	a.Scale(2) - Each value of the Matrix "a" will be increased by factor of 2.
Offset(value)	All the elements of the Matrix are offset by the specified value (New value = original value + Offset).		value : the required offset value. This is of data type REAL.	a.Offset(5) - Each value of the Matrix "a" will be increased by 5.
Copy(Matrix)	The Matrix is resized to be the same as the specified Matrix and all the elements are copied into the new Matrix.		Matrix: the name of the Matrix to copy from. This is an Matrix class.	PreVals.Copy(a) - The values in Matrix "a" are copied into the Matrix "PreVals". If required, "PreVals" is resized to match the size of "a".
IsEqual(Matrix)	This compares the current Matrix with the specified Matrix data, if the matrix sizes match and each element of the Matrix are equal, the function returns the value, True.	Bit	Matrix: the name of the Matrix to compare with. This is a Matrix class.	EqualOK = PreVals.IsEqual(a) - Returns true if the size of "PreVals" and "a" are equal and the values in Matrix "PreVals" are equal to the values of the Matrix "a".
GetRow(RowIndex, Array)	This retrieves the values the specified row of the matrix, the values are stored in the specified array. Array size is set to the number of columns. Return false if invalid RowIndex.	Bit	RowIndex: the index of the required Row entry in the matrix (Note: index starts at zero). This is of data type LONG. Array: the name of the array to stored the retrieved information. This is an Array class.	a.GetRow(0, TestRow)
GetCol(ColIndex, Array)	This retrieves the values the specified column of the matrix, the values are stored in the specified array. Array size is set to the number of rows. Return false if invalid ColIndex.	Bit	ColIndex: the index of the required column entry in the matrix (Note: index starts at zero). This is of data type LONG. Array: the name of the array to stored the retrieved information. This is an Array class.	a.GetCol(0, TestCol)
SetRow(RowIndex, Array)	This sets the values at the specified row in the matrix, with values from the specified array. The matrix row length must equal to the array length, otherwise it will report an error. Return false if invalid RowIndex or length of Array does not match number of columns.	Bit	RowIndex: the index of the required Row entry in the matrix (Note: index starts at zero). This is of data type LONG. Array: the name of the array that contains the values. This is an Array class.	a.SetRow(1, TestRow)
SetCol(ColIndex, Array)	This sets the values at the specified column in the matrix, with values from the specified array. The matrix column length must equal to the array length, otherwise it will report an error. Return false if invalid ColIndex or length of Array does not match number of rows.	Bit	ColIndex: the index of the required column entry in the matrix (Note: index starts at zero). This is of data type LONG. Array: the name of the array that contains the values. This is an Array class.	a.SetCol(1, TestCol)
SwapRows(RowIndex1, RowIndex2) Available from Build 139.30807. (Also SwopRows)	This swaps the contents of the specified rows in the matrix. The row indexes must be valid, otherwise it will report an error.		RowIndex1: the index of one of the required rows in the matrix for the swap (Note: index starts at zero). This is of data type LONG. RowIndex2: the index of the other required row in the matrix for the swap.	a.SwapRows(1, 3)
SwapCols(ColIndex1, ColIndex2) Available from Build 139.30807.(Also SwopCols)	This swaps the contents of the specified columns in the matrix. The column indexes must be valid, otherwise it will report an error.		ColIndex1: the index of one of the required columns in the matrix for the swap (Note: index starts at zero). This is of data type LONG. ColIndex2: the index of the other required column in the matrix for the swap.	a.SwapCols(0, 5)
Functions acting on Rows (Available from Build 139.30807.)
RowSetAll(RowIndex, value)	This sets all the elements of the specified row to the specified value.		RowIndex: the index of the required Row entry in the matrix. This is of data type LONG. value : the required value. This is of data type REAL.	a.RowSetAll(3, 0)
RowScale(RowIndex, value)	All the elements of the specified row are scaled by the specified value (New value = original value * Scale).		RowIndex: the index of the required Row entry in the matrix. This is of data type LONG. value : the required scaling factor. This is of data type REAL.	a.RowScale(0, 2)
RowOffset(RowIndex, value)	All the elements of the specified row are offset by the specified value (New value = original value + Offset).		RowIndex: the index of the required Row entry in the matrix. This is of data type LONG. value : the required offset value. This is of data type REAL.	a.RowOffset(0, 5)
RowSum(RowIndex)	This calculates the sum of all elements of the specified row.	Real	RowIndex: the index of the required Row entry in the matrix. This is of data type LONG.	e = a.RowSum(0)
RowAvg(RowIndex)	This calculates the average of all elements of the specified row.	Real	RowIndex: the index of the required Row entry in the matrix. This is of data type LONG.	e = a.RowAvg(0)
RowMin(RowIndex)	This returns the minimum value of all elements of the specified row.	Real	RowIndex: the index of the required Row entry in the matrix. This is of data type LONG.	e = a.RowMin(0)
RowMinIndex(RowIndex)	This returns the index of the minimum value of the specified row. If multiple entries of equal minimum value, the first row index is returned. Return value is -1 for empty matrix.	integer	RowIndex: the index of the required Row entry in the matrix. This is of data type LONG.	d = a.RowMinIndex(0)
RowMax(RowIndex)	This returns the maximum value of all elements of the specified row.	Real	RowIndex: the index of the required Row entry in the matrix. This is of data type LONG.	e = a.RowMax(0)
RowMaxIndex(RowIndex)	This returns the index of the maximum value of the specified row. If multiple entries of equal maximum value, the first row index is returned. Return value is -1 for empty matrix.	integer	RowIndex: the index of the required Row entry in the matrix. This is of data type LONG.	d = a.RowMaxIndex(0)
RowNorm(RowIndex)	This normalises the contents of of the specified row such that the sum is 1.		RowIndex: the index of the required Row entry in the matrix. This is of data type LONG.	a.RowNorm(0)
RowReverse(RowIndex)	This reverses the sequence of all elements of the specified row.		RowIndex: the index of the required Row entry in the matrix. This is of data type LONG.	a.RowReverse(0)
RowSort(RowIndex, Ascending/Descending)	This re-arranges all elements in the specified row in ascending / descending order.		RowIndex: the index of the required Row entry in the matrix. This is of data type LONG. 0: Descending order, 1: Ascending order	a.RowSort(true)
RowIsSorted(RowIndex, Ascending/Descending)	This checks if the specified row is sorted in ascending / descending order. Returns True if specified row is sorted in the specified order.	Bit	RowIndex: the index of the required Row entry in the matrix. This is of data type LONG. 0: Descending order, 1: Ascending order	SortOK = a.RowIsSorted(0, 1)
Functions acting on Columns (Available from Build 139.30807 or 139.31866.)
ColSetAll(ColIndex, value)	This sets all the elements of the specified column to the specified value.		ColIndex: the index of the required Column entry in the matrix. This is of data type LONG. value : the required value. This is of data type REAL.	a.ColSetAll(3, 0)
ColScale(ColIndex, value)	All the elements of the specified column are scaled by the specified value (New value = original value * Scale).		ColIndex: the index of the required Column entry in the matrix. This is of data type LONG. value : the required scaling factor. This is of data type REAL.	a.ColScale(0, 2)
ColOffset(ColIndex, value)	All the elements of the specified column are offset by the specified value (New value = original value + Offset).		ColIndex: the index of the required Column entry in the matrix. This is of data type LONG. value : the required offset value. This is of data type REAL.	a.ColOffset(0, 5)
ColSum(ColIndex)	This calculates the sum of all elements of the specified column.	Real	ColIndex: the index of the required Column entry in the matrix. This is of data type LONG.	e = a.ColSum(0)
ColAvg(ColIndex)	This calculates the average of all elements of the specified column.	Real	ColIndex: the index of the required Column entry in the matrix. This is of data type LONG.	e = a.ColAvg(0)
ColMin(ColIndex)	This returns the minimum value of all elements of the specified column.	Real	ColIndex: the index of the required Column entry in the matrix. This is of data type LONG.	e = a.ColMin(0)
ColMinIndex(ColIndex)	This returns the index of the minimum value of the specified column. If multiple entries of equal minimum value, the first column index is returned. Return value is -1 for empty matrix.	integer	ColIndex: the index of the required Column entry in the matrix. This is of data type LONG.	d = a.ColMinIndex(0)
ColMax(ColIndex)	This returns the maximum value of all elements of the specified column.	Real	ColIndex: the index of the required Column entry in the matrix. This is of data type LONG.	e = a.ColMax(0)
ColMaxIndex(ColIndex)	This returns the index of the maximum value of the specified column. If multiple entries of equal maximum value, the first column index is returned. Return value is -1 for empty matrix.	integer	ColIndex: the index of the required Column entry in the matrix. This is of data type LONG.	d = a.ColMaxIndex(0)
Matrix arithmetic functions
Add(Matrix)	This function performs addition between current matrix and a specified matrix. New value for each element in current matrix = value in current Matrix + specified Matrix. The two Matrices must be the same size. If they are not the same size then return value is false, a runtime error is reported and current matrix values are left unchanged.	Bit	Matrix: the name of the specified Matrix. This is a Matrix class.	OK = M.Add(M1) (each element in M = M + M1)
Sub(Matrix)	This function performs subtraction between current matrix and a specified matrix. New value for each element in current matrix = value in current Matrix - specified Matrix. The two Matrices must be the same size. If they are not the same size then return value is false, a runtime error is reported and current matrix values are left unchanged.	Bit	Matrix: the name of the specified Matrix. This is a Matrix class.	OK = M.Sub(M1) (each element in M = M - M1)
Mult(Matrix)	This function performs multiplication between current matrix and a specified matrix. New value for each element in current matrix = value in current Matrix * specified Matrix. The two Matrices must be the same size. If they are not the same size then return value is false, a runtime error is reported and current matrix values are left unchanged.	Bit	Matrix: the name of the specified Matrix. This is a Matrix class.	OK = M.Mult(M1) (each element in M = M * M1)
Div(Matrix)	This function performs division between current matrix and a specified matrix. New value for each element in current matrix = value in current Matrix / specified Matrix. The two Matrices must be the same size. If they are not the same size then return value is false, a runtime error is reported and current matrix values are left unchanged.	Bit	Matrix: the name of the specified Matrix. This is a Matrix class.	OK = M.Div(M1) (each element in M = M / M1)
MultMatrix(Matrix)	Matrix multiplication for matrix of different size, but the number of Rows in the specified Matrix must match the number of columns of the current matrix. The resulting matrix is resized.	Bit	Matrix: the name of the specified Matrix. This is a Matrix class.	MultMatrixOK = L.MultMatrix(M1) - If Matrix "L" is 3x2 and Matrix "M1" is 2x4, resulting Matrix "L" is resized to 3x4.
MultArray(Array)	Matrix by Array multiplication, the Array is treated as a matrix with one of the dimensions equal to 1. The matrix column length must match the array length.	Bit	Array: the name of the specified Array. This is an Array class.	MultArrayOK = L.MultArray(xA) - the number of columns in Matrix "L" must equal to the array length of "xA"
MultLeftArray(Array) Available from Build 139.32684.	Array by Matrix multiplication, the Array is treated as a matrix with one of the dimensions equal to 1. The matrix row length must match the array length.	Bit	Array: the name of the specified Array. This is an Array class.	MultArrayOK = L.MultLeftArray(xA) - the number of rows in Matrix "L" must equal to the array length of "xA"
Transpose()	Transposes the matrix.			M.Transpose()
Determinant()	Calculates and returns Determinant of the matrix. The matrix must be square, if not a runtime error is given and the value of zero is returned. For a square matrix, a result of zero indicates matrix is Singular and cannot be inverted. LU Decomposition method is used to calculate the Determinant.	Real	None	Det = I.Determinant()
Invert()	Inverts the matrix. The matrix must be square, if not a runtime error is given and "false" is returned. If unable to complete invert due to matrix being Singular (determinant = 0), returns false but still changes matrix values. LU Decomposition method is used to calculate the inverse of the matrix.	Bit	None	InvertOK = Iv1.Invert()
Solve(Array)	Solves a system of equations (solve x for Ax = b, where A is a matrix and b and x are arrays). The matrix must be square and the length of the array must be the same the matrix, if not runtime error is given and "false" is returned. LU Decomposition and back substitution method is used.	Bit	Array: the name of the specified RHS (e.g. b), which is overwritten by the result (e.g. x). This is an Array class.	SolveOK = A.Solve(b)
Copy versions of matrix arithmetic functions (First action is to make a copy of the supplied Matrix1)
CopyAdd(Matrix1, Matrix2)	Makes a copy of the supplied Matrix1 and then calls Add(Matrix2). The two Matrices must be the same size, otherwise value remains unchanged and error is returned.	Bit	Matrix1: the name of the first specified Matrix. This is a Matrix class. Matrix2: the name of the second specified Matrix. This is a Matrix class.	OK = M.CopyAdd(M1, M2) (each element in M = M1 + M2)
CopySub(Matrix1, Matrix2)	Makes a copy of the supplied Matrix1 and then calls Sub(Matrix2). The two Matrices must be the same size, otherwise value remains unchanged and error is returned.	Bit	Matrix1: the name of the first specified Matrix. This is a Matrix class. Matrix2: the name of the second specified Matrix. This is a Matrix class.	OK = M.CopySub(M1, M2) (each element in M = M1 - M2)
CopyMult(Matrix1, Matrix2)	Makes a copy of the supplied Matrix1 and then calls Mult(Matrix2). The two Matrices must be the same size, otherwise value remains unchanged and error is returned.	Bit	Matrix1: the name of the first specified Matrix. This is a Matrix class. Matrix2: the name of the second specified Matrix. This is a Matrix class.	OK = M.CopyMult(M1, M2) (each element in M = M1 * M2)
CopyDiv(Matrix1, Matrix2)	Makes a copy of the supplied Matrix1 and then calls Div(Matrix2). The two Matrices must be the same size, otherwise value remains unchanged and error is returned.	Bit	Matrix1: the name of the first specified Matrix. This is a Matrix class. Matrix2: the name of the second specified Matrix. This is a Matrix class.	OK = M.CopyDiv(M1, M2) (each element in M = M1 / M2)
CopyMultMatrix(Matrix1, Matrix2)	This function performs multiplication between two matrices and stores the values in a new matrix(current matrix). The matrices can be of different size, but the number of Rows in the specified Matrix must match the number of columns of the current matrix. The resulting matrix is resized.	Bit	Matrix1: the name of the first specified Matrix. This is a Matrix class. Matrix2: the name of the second specified Matrix. This is a Matrix class.	MultMatrixOK = M.CopyMultMatrix(L,M1) - If Matrix "L" is 3x2 and Matrix "M1" is 2x4, resulting Matrix "M" is resized to 3x4.
CopyMultArray(Matrix, Array)	This function performs multiplication between a matrix and an array. The results are stored in a new matrix(current matrix). Matrix by Array multiplication, the Array is treated as a matrix with one of the dimensions equal to 1. The matrix column length must match the array length.	Bit	Matrix: the name of the first specified Matrix. This is a Matrix class. Array: the name of the specified Array. This is an Array class.	MultArrayOK = M.CopyMultArray(L, xA) - the number of columns in Matrix "L" must equal to the array length of "xA"
CopyMultLeftArray(Matrix, Array) Available from Build 139.32684.	This function performs multiplication between an array and a matrix. The results are stored in a new matrix(current matrix). Array by Matrix multiplication, the Array is treated as a matrix with one of the dimensions equal to 1. The matrix row length must match the array length.	Bit	Matrix: the name of the first specified Matrix. This is a Matrix class. Array: the name of the specified Array. This is an Array class.	MultArrayOK = M.CopyMultLeftArray(L, xA) - the number of rows in Matrix "L" must equal to the array length of "xA"
CopyTranspose(Matrix)	Makes a copy of the supplied Matrix and then calls Transpose() so that original matrix is left unchanged.		Matrix: the name of the specified Matrix. This is a Matrix class.	PreVals.CopyTranspose(a) - The values in Matrix "a" are copied and transposed into the Matrix "PreVals".
CopyInvert(Matrix)	Makes a copy of the supplied Matrix and then calls Invert() so that original supplied Matrix is left unchanged.	Bit	Matrix: the name of the specified Matrix. This is a Matrix class.	InvertOK = CIv1.Invert(Iv1)
CopySolve(Matrix, Array)	Makes a copy of the supplied Matrix and then calls Solve(Array) so that original supplied Matrix is left unchanged.	Bit	Matrix: the name of the specified Matrix. This is a Matrix class. Array: the name of the specified RHS, which is overwritten. This is an Array class.	SolveOK = M.CopySolve(A, X)

Watch (Displaying Matrix values)

The watch function can be used to display the matrix values on the access window. The matrix Watch function has been greatly improved in Build138.24698.

For example using Watch GypsumSolubility@ will display the following in the Access window M1 tab:

Syntax (for Build138.24698 or later) :

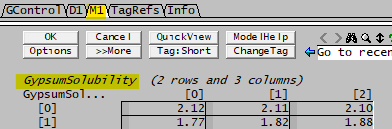
To add the matrix display to the access window, the Syntax is "Watch MMM", where MMM is the name of the Matrix, in the example above, it is GypsumSolubility
If the "@" symbol is included (e.g. "Watch MMM@"), then the matrix elements will be read only fields in the access window (as per example above).
The matrix values will be added to a new tab called M1, other Mx tabs may be added if required. These tabs are auto generated, user cannot rename these tabs.
The values for the matrix are shown after the project has started solving.
The values are shown in a grid view on the M_x tab pages. (Improved from the old single list view).
The matrix size is display above matrix, in the example above, it is (GypsumSolubility (2 rows and 3 columns))
The matrix row and column headings are shown as row count and column count, these are generated automatically, they cannot be customised by the user.
The maximum size for the grid view display is 1000 rows x 50 columns, but all the possible tags always work even if they are not visible on the access window display.
If you have referenced a tag from the matrix (e.g. in trend), and then reduced the matrix size, it will return NAN (*) or become an invalid tag (depending on when matrix is resized).

Syntax for earlier builds To make the matrix variables visible in the access window the Watch command can be used.

Individual elements in the matrix can be made visible - e.g. "Watch A[2,1]" or "Watch A@[2,1]" for element at row 2 and column 1.
A range of matrix elements can be made visible - e.g. "Watch A[All,5,2]" shows first 5 rows and 2 columns.
If the "@" symbol is included, then the matrix elements will be read only fields in the access window.

Matrix with Constant Values

The user may declare a matrix with a set of constant values. This allows the user to set up a table with known values for direct use (for example, as a lookup tabnle). It can be a useful alternative to reading values from a CSV file. Once defined, the contents or size of this constant Matrix cannot be changed. Where a number is not specified for an entry, 0 is assumed. The contents of the array are not saved as they are defined in the code. From Build 139.32217, the list can include system constants (for example NAN or PI), or user defined constants. From Build 139.32325 the const keyword should be used, otherwise a load warning (or error) is given.

The syntax is:

const Matrix  LookupTable = {{a1,a2,a3,....}, {b1,b2,b3,....}, {c1,c2,c3,....}} ;Syntax from Build 139.32325
Matrix  LookupTable = {{a1,a2,a3,....}, {b1,b2,b3,....}, {c1,c2,c3,....}}       ;Syntax before Build 139.32325
;where a1, a2, b1, etc. are real numbers or constants.

Notes:

Each group is a row, so {a1,a2,a3,....} is the first row of the Matrix.
If the number of elements in each row differs, the maximum number is used to set the number of colums in the Matrix. The missing elements are initialised to zero.
The Matrix is Read Only so data elements cannot be set, the Matrix resized, etc.

Caution

Using a GetAt within a SetAt can sometimes fail.

;For example:
a.SetAt(i, j, a.GetAt(i+1, j))  ;This can sometimes fail

;The solution is to use a temporary variable to first retrieve the GetAt value and then call SetAt as follows:
Real   Tmp
Tmp = a.GetAt(i+1, j)
a.SetAt(i, j, Tmp)

Solving Systems of Equations

For a single solution of an equation AX = B, where B is an array, use A.Solve(B). Both the original matrix and the RHS are overwritten, so the solution is now in the array B.

If you don't want to overwrite the original matrix, use M.CopySolve(A, B). B is again overwritten with the solution; if you don't want this, make a copy first.

For solving repeated sets of equations with the same fixed matrix, calculate the inverse (do this in OnInitialize), then use matrix multiplication via MultArray or CopyMultArray.

Examples

Examples 1 and 2

Example 1

Example 2

Displaying the Matrix value (Example 2)

Matrix       TestMatrix, TestMatrix1, TestMatrix2, TestMatrix3
;Matrix      Table1 = { {2, 5, 10}, {1, 3, 6} } ;Old syntax before Build 139.32325
const Matrix Table1 = { {2, 5, 10}, {1, 3, 6} }
Real         Col1Sum@, SumV@, AverageV@, MinimumV@, MaximumV@
Long         RowCount@, ColCount@
;Array       TestRowValue = {25, 30, 35} ;Old syntax before Build 139.32325
const Array  TestRowValue = {25, 30, 35}
const Array  TestColValue = {5, 10}
Array        TestRow, TestCol
Bit          OK@, OK2@
 
Sub InitialiseSolution()
  TestMatrix.Copy(Table1)
  SumV     = TestMatrix.Sum()
  AverageV = TestMatrix.Avg()
  MinimumV = TestMatrix.Min()
  MaximumV = TestMatrix.Max() 
  TestMatrix.Scale(2)
  TestMatrix.Transpose()
  RowCount = TestMatrix.GetRowCount()
  ColCount = TestMatrix.GetColCount()
  TestMatrix1.SetSize(2,3)
  TestMatrix2.Copy(Table1)
  TestMatrix3.SetSize(2,3)
  TestMatrix2.GetRow(0, TestRow)
  TestMatrix2.GetCol(0, TestCol)
  TestMatrix1.SetRow(1, TestRowValue)
  TestMatrix1.SetCol(0, TestColValue)
  TestMatrix3.Add(TestMatrix2)
  TestMatrix3.Sub(TestMatrix2)
  TestMatrix3.Mult(TestMatrix2)
  TestMatrix3.Div(TestMatrix2)
  OK  = TestMatrix2.MultMatrix(TestMatrix)
  OK2 = TestMatrix1.MultArray(TestRowValue)
EndSub

EndFile

Matrix    a
String    ProjectFolder, CsvFilename@
Real      d*, Col1Sum@
Long      RowCount@, ColCount@, i
Bit       SaveNow*, OK@, CopyToClipboard*
 
Watch a

Sub InitialiseSolution()
  ProjectFolder = ["PlantModel.System.PrjFolder"]
  CsvFilename = Concatenate(ProjectFolder, "\test.csv")
  a.SetSize(5, 3)
  a.setat(2, 2, 2.2)  
  a.setat(0, 1, 0.1)  
  a.setat(4, 1, 4.1)  
  d = 2^0.5
  RowCount = a.GetRowCount()
  ColCount = a.GetColCount()
EndSub

  a.SetAt(1, 1, d)
  a.SetAt(2, 2, ["Autoclave.QProd.QM:Ph.MgSO4(aq) (t/h)"])
  i = 0
  Col1Sum = 0.0
  while (i<RowCount)
    Col1Sum = Col1Sum + a.GetAt(i, 1)
    i = i + 1
  endWhile
  
  if (SaveNow)
    SaveNow = false
    OK = a.Save(CsvFilename)
    if (NOT OK)
        LogError(Concatenate("Matrix data not saved to file ", CsvFilename))
    endif  
  endif 
  
  if (CopyToClipboard)
    CopyToClipboard = false
    a.CopyToClipboard()
  endif
EndFile

Example 3 - Table Look up using Array and Matrix

Table lookup using Array and Matrix

Matrix Class

Contents

Description

Data Members

Member Functions

Watch (Displaying Matrix values)

Matrix with Constant Values

Caution

Solving Systems of Equations

Examples

Examples 1 and 2

Example 3 - Table Look up using Array and Matrix

Navigation menu

Matrix Class

Description

Data Members

Member Functions

Watch (Displaying Matrix values)

Matrix with Constant Values

Caution

Solving Systems of Equations

Examples

Examples 1 and 2

Example 3 - Table Look up using Array and Matrix

Navigation menu

Search