Stream Properties using Standard Method
Navigation: Models ➔ Species Models ➔ Standard Species Model ➔ Stream Properties Calculations
| Standard Species Model | Stream Properties | Special Cases | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Standard Species Model | Stream Properties Calculations | Density | Heat of Formation | Heat of Dilution | Specific Heat (Cp) | Solubility | Boiling Point Elevation | pH | Charge | Steam and Water | Sulfuric Acid |
Related Links: Material Flow Section, Model Examples
Introduction
Given the following stream make up at 25°C and atmospheric pressure, stream properties are calculated in SysCAD using the Standard species model, primarily a mass weighted mean method. These calculations are illustrated using the example below:
Table 1 Stream Make Up
| Stream Make Up | Mass Flow | Mass Frac | Mole Flow |
|---|---|---|---|
| kg/h | wt Frac | kmol/h | |
| CaCO3(s) | 200.00 | 0.20 | 1.998 |
| SiO2(s) | 300.00 | 0.30 | 4.993 |
| H2O(l) | 400.00 | 0.40 | 22.203 |
| H2SO4(aq) | 80.00 | 0.08 | 0.816 |
| CO2(g) | 10.00 | 0.01 | 0.227 |
| N2(g) | 10.00 | 0.01 | 0.357 |
| Total | 1000.00 | 1.00 | 30.594 |
Table 2 Species Data entered into the SysCAD Species Database.
| Species | Density (kg/m3 | Hf at 25°C (J/mol) | S at 25°C (J/mol.K) | Cp Equation (kJ/kmol.K) | Temp Range (K) |
|---|---|---|---|---|---|
| CaCO3(s) | 2650 | -1208352 | 92.9 | HTE_Cp(-9122, 23.8351, 3.2146, 5.1569) | 298 - 1200 |
| SiO2(s) | 2650 | -911550 | 41.84 | HTE_Cp(-8654, 19.1651, -0.5456, 8.8977) | 298 - 2000 |
| H2SO4(aq) | 1841 | -886513 | 20.1 | HTE_Cp(-7762, 19.1799, 23.2471, -0.0679) | 298 - 500 |
| CO2(g) | 1.8 | -393505.213 | 213.74 | Poly_Cp(19.7961, 0.07344, -5.600221e-05, 1.71541e-08) | 298.15 - 1000 |
| N2(g) | 1.15 | 0 | 191.61 | Poly_Cp(31.1513, -0.0135659, 2.67968e-05, -1.16817e-08) | 298 - 1000 |
Note:
Properties for H2O are NOT entered by the user - these values are calculated within SysCAD. (See Water and Steam Properties.)
From Heat Capacity (Cp), we will find the Cp equation formats for the HTE_Cp and Poly_Cp as follows:
HTE_Cp(a,b,c,d) :
- [math]\displaystyle{ C_p = 4.186\left (b+2c.10^{-3}T-\frac{d.10^5}{T^2} \right ) }[/math]
Poly_Cp(a,b,c,d):
- [math]\displaystyle{ C_p = a+bT+cT^2+dT^3 }[/math]
The Cp values for each individual species are calculated at the specified temperature, in K, using the above equations, and Enthalpies ('Hs') are calculated by integrating the above equations from Reference temperature 273.15K to the specified temperature. The results of these calculations are presented in Table 3. (Note that since the reference temperature of 273.15K is less than Ts (Start Temperature) of 298.15K, to calculate Hs the Cp at 298.15K will be multiplied by (298.15-273.15). See Heat Capacity (Cp) for more information.)
Table 3 Species Properties Summary at 25°C and 1 Atmospheric Pressure
| Species Properties |
MW kg/kgmol |
Density kg/m3 |
H@T kJ/kg |
Hs kJ/kg |
S@T kJ/kg.C |
Cp kJ/kg.C |
|---|---|---|---|---|---|---|
| CaCO3(s) | 100.09 | 2650.00 | -12073.03 | 20.85 | 0.93 | 0.83 |
| SiO2(s) | 60.08 | 2650.00 | -15171.18 | 15.36 | 0.70 | 0.62 |
| H2O(l) | 18.02 | 997.05 | -15865.97 | 104.87 | 3.89 | 4.18 |
| H2SO4(aq) | 98.08 | 1841.00 | -9038.81 | 35.33 | 0.20 | 1.41 |
| CO2(g) | 44.01 | 1.80 | -8941.37 | 21.11 | 4.86 | 0.84 |
| N2(g) | 28.01 | 1.15 | 0 | 26.04 | 6.84 | 1.04 |
Notes:
- The user specifies properties of individual species (compounds) in the SysCAD Species Database.
- Hs and Cp values are derived from the Cp equations.
- The individual species properties at different Temperature and Pressures can be obtained via the menu command Species -- View Properties. (Refer to Species Properties ($SDB) for more information.)
Table 4 Stream Properties Summary
| 0°C, 1 atm | 25°C, 1 atm | 50°C, 1 atm | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stream Properties | MW | Density | Hf | S | Hs | Hf | S | Hs | Cp | Hf | S | Hs | Cp |
| kg/kgmol | kg/m3 | kJ/kg | kJ/kg.C | kJ/kg | kJ/kg | kJ/kg.C | kJ/kg | kJ/kg.C | kJ/kg | kJ/kg.C | kJ/kg | kJ/kg.C | |
| Total | 32.69 | 67.00 | -14178.89 | 1.90 | 0 | -14124.87 | 2.09 | 54.02 | 2.16 | -14070.43 | 2.21 | 108.46 | 2.20 |
| Solid Phase | 71.52 | 2650.00 | - | - | 0 | - | - | 17.56 | 0.70 | - | - | 36.15 | 0.78 |
| Liquid Phase | 20.85 | 1079.53 | - | - | 0 | - | - | 93.28 | 3.72 | - | - | 186.34 | 3.73 |
| Vapour Phase | 34.24 | 1.40 | - | - | 0 | - | - | 23.58 | 0.94 | - | - | 47.31 | 0.96 |
| Slurry (Sol + Liq) | 32.66 | 1547.41 | - | - | 0 | - | - | 54.65 | 2.18 | - | - | 109.71 | 2.22 |
The methods used to calculate these values are shown in the following headings:
Stream Molecular Weight
[math]\displaystyle{ Stream Molecular Weight = \cfrac{\sum{m_i}}{\sum{n_i}} }[/math]
where:
- mi = mass of individual species
- ni = mole of individual species
So for the above example:
[math]\displaystyle{ Stream Molecular Weight = \cfrac{1000kg}{30.594kgmoles} = 32.69kg/kgmol }[/math]
Note:
SysCAD uses the atomic weight of the elements and the species definition in the Species Database to calculate the Molecular weight of each species.
Stream Density
The Stream Density is calculated as:
[math]\displaystyle{ \cfrac{Total\ mass}{Total\ volume} = \cfrac{\sum{m_i}}{\sum{\frac{m_i}{\rho_i}}} }[/math]
where:
- mi = mass of individual species
- ρi = density of individual species (for vapours this is the partial pressure)
[math]\displaystyle{ \mathbf{\mathit{Stream Density = 1000 / (200/2650 + 300/2650 + 400/997.04 + 80/1841 + 10/1.80 + 10/1.15) = 67.00 kg/m^3}} }[/math]
Likewise,
- [math]\displaystyle{ \mathbf{\mathit{Solid Density = Total Solid Mass / Total Solid Volume = 500 / (200/2650 + 300/2650) = 2650 kg/m^2}} }[/math]
- [math]\displaystyle{ \mathbf{\mathit{Liquid Density = Total Liquid Mass / Total Liquid Volume = 1079.53 kg/m^2}} }[/math]
- [math]\displaystyle{ \mathbf{\mathit{Vapour Density = Total Vapour Mass / Total Vapour Volume = 1.40 kg/m^2}} }[/math]
- [math]\displaystyle{ \mathbf{\mathit{Slurry Density = Total (Solid + Liquid) Mass / Total (Solid + Liquid) Volume = 1547.41 kg/m^2}} }[/math]
See also: Density and Volume display for mixtures
For solution density calculations requiring correction functions, please see Density Correction for Solutions & Data Fitting.
- The gas phase species are handled separately. In a vapour mixture, all species occupy the same volume. The densities are evaluated at the partial pressure of the species in question and the mixture density is just the sum of the species densities.
- For mixtures with more than one phase present, the multiphase density is
[math]\displaystyle{ \rho = \sum M_p/\sum_p M_p/\rho_p }[/math]
Vapour Phase Density
- In earlier versions of SysCAD (Build 135 and earlier), the gas phase density for mixtures was evaluated at the total pressure for each species, the corresponding specific volumes being mass-weight averaged. For ideal gases, this is equivalent to adding the densities. For non-ideal gases, particularly when one species is at saturation, this can lead to errors. As such, the partial pressure is used. This gives improved results for density and volume flows of vapours where there are multiple gas species (including steam) in the mixture.
Stream Enthalpy values (Hs)
Stream Enthalpy values are calculated using the mass weighted mean method. Using values in Table 3 Species Properties Summary, we have:
| Hs @25 | = | Stream Enthalpy (Heat Content) |
| = | [math]\displaystyle{ \mathbf{\mathit{ \sum mf_i * Hs_i }} }[/math] | |
| where mfi and Hsi are the mass fraction and enthalpy of individual species, respectively | ||
| = | [math]\displaystyle{ \mathbf{\mathit{ 0.2*20.85 + 0.3*15.36 + 0.4*104.87 + 0.08*35.33 + 0.01*21.11 + 0.01*26.04}} }[/math] | |
| = | [math]\displaystyle{ \mathbf{\mathit{ 54.02 kJ/kg}} }[/math] | |
| SmsHs @25 | = Solids Enthalpy |
| = [math]\displaystyle{ \mathbf{\mathit{ \sum mf_{i \ solids} * Hs_i = 0.2/0.5*20.85 + 0.3/0.5*15.36 = 17.56 kJ/kg }} }[/math] | |
| where mfi solids is the mass fraction of solids in the solid phase |
| LmsHs @25 | = Liquid Enthalpy |
| = [math]\displaystyle{ \mathbf{\mathit{ \sum mf_{i \ liquids} * Hs_i = 0.4/0.48*104.87 + 0.08/0.48*35.33 = 93.28 kJ/kg }} }[/math] | |
| where mfi liquids is the mass fraction of liquids in the liquid phase |
| VmsHs @25 | = Vapour Enthalpy |
| = [math]\displaystyle{ \mathbf{\mathit{ \sum mf_{i \ vapour} * Hs_i = 0.01/0.02*21.11 + 0.01/0.02*26.04 = 23.58 kJ/kg }} }[/math] | |
| where mfi vapour is the mass fraction of vapour in the vapour phase |
| SLmsHs @25 | = Slurry Enthalpy |
| = [math]\displaystyle{ \mathbf{\mathit{ \sum mf_{i \ slurry} * Hs_i }} }[/math] | |
| where mfi slurry is the mass fraction of liquid/solid in the slurry (liquid+solid) phase | |
| = [math]\displaystyle{ \mathbf{\mathit{0.2/0.98*20.85 + 0.3/0.98*15.36 + 0.4/0.98*104.87 + 0.08/0.98*35.33}} }[/math] | |
| = [math]\displaystyle{ \mathbf{\mathit{54.65 kJ/kg}} }[/math] |
Stream Specific Heat values (Cp)
Stream Specific Heat values are calculated using the mass weighted mean method. Using values in Table 3 Species Properties Summary, we have:
| Cp @25 | = Stream Cp |
| = [math]\displaystyle{ \mathbf{\mathit{ \sum mf_i * Cp_i}} }[/math] | |
| where mfi and Cpi are the mass fraction and Cp of individual species, respectively | |
| = [math]\displaystyle{ \mathbf{\mathit{0.2*0.83 + 0.3*0.62 + 0.4*4.18 + 0.08*1.41 + 0.01*0.84 + 0.01*1.04 }} }[/math] | |
| = [math]\displaystyle{ \mathbf{\mathit{2.16 kJ/kg.C}} }[/math] |
| SmsCp @25 | = Solids Cp |
| = [math]\displaystyle{ \mathbf{\mathit{ \sum mf_{i \ solids} * Cp_i = 0.2/0.5*0.83 + 0.3/0.5*0.62 = 0.70 kJ/kg.C }} }[/math] | |
| where mfi solids is the mass fraction of solids in the solid phase |
| LmsCp @25 | = Liquid Cp |
| = [math]\displaystyle{ \mathbf{\mathit{ \sum mf_{i \ liquids} * Cp_i = 0.4/0.48*4.18 + 0.08/0.48*1.41 = 3.72 kJ/kg.C }} }[/math] | |
| where mfi liquids is the mass fraction of liquids in the liquid phase |
| VmsCp @25 | = Vapour Cp |
| = [math]\displaystyle{ \mathbf{\mathit{ \sum mf_{i \ vapour} * Cp_i = 0.01/0.02*0.84 + 0.01/0.02*1.04 = 0.94 kJ/kg.C}} }[/math] | |
| where mfi vapour is the mass fraction of vapour in the vapour phase |
| SLmsCp @25 | = Slurry Cp |
| = [math]\displaystyle{ \mathbf{\mathit{ \sum mf_{i \ slurry} * Cp_i }} }[/math] | |
| where mfi slurry is the mass fraction of liquid/solid in the slurry (liquid+solid) phase | |
| = [math]\displaystyle{ \mathbf{\mathit{0.2/0.98*0.83 + 0.3/0.98*0.62 + 0.4/0.98*4.18 + 0.08/0.98*1.41}} }[/math] | |
| = [math]\displaystyle{ \mathbf{\mathit{2.18 kJ/kg.C}} }[/math] |
Stream Heat of Formation values (Hf)
Consider the stream is at 50°C; the stream enthalpy calculations are as follows:
Stream Heat of Formation values are calculated using the mass weighted mean method. Generally, the Heat of Formation data available are at 25°C. Thus, using these values, stream Hf at 25°C is calculated.
From Table 3 Species Properties Summary, we have:
| Stream Hf 25°C | = [math]\displaystyle{ \sum mf_i * H_{f \ i}^{25} }[/math]
| |||
| [math]\displaystyle{ \mathbf{\mathit{= 0.2*-12073.03 + 0.3*-15171.18 + 0.4*-15865.97 + 0.08*-9038.81 + 0.01*-8941.31 + 0.01*0}} }[/math] | ||||
| [math]\displaystyle{ \mathbf{\mathit{= -14124.87 kJ/kg}} }[/math] |
| Stream Hf 0°C | = [math]\displaystyle{ \mathbf{\mathit{ H_f^{25} - \sum \int\limits_{0}^{25}Cp_i.dT}} }[/math] |
| = [math]\displaystyle{ \mathbf{\mathit{H_f 25^{\circ}C - (Hs 25^{\circ}C- Hs 0^{\circ}C)}} }[/math] | |
| = [math]\displaystyle{ \mathbf{\mathit{-14124.87 - (54.02 - 0)}} }[/math] (See Table 4 Stream Properties Summary) | |
| = [math]\displaystyle{ \mathbf{\mathit{-14178.89 kJ/kg}} }[/math] |
| Stream Hf 50°C | = [math]\displaystyle{ \mathbf{\mathit{ H_f^0 + \sum \int\limits_{0}^{50}Cp_i.dT}} }[/math] |
| = [math]\displaystyle{ \mathbf{\mathit{H_f 0^{\circ}C + (Hs 50^{\circ}C - Hs 0^{\circ}C)}} }[/math] | |
| = [math]\displaystyle{ \mathbf{\mathit{-14178.88 + (108.46 - 0)}} }[/math] (See Table 4 Stream Properties Summary) | |
| = [math]\displaystyle{ \mathbf{\mathit{-14070.42 kJ/kg}} }[/math] |
Enthalpy Change (Hs) and (Hz)
Hs is the enthalpy change (excluding phase change) from 0°C to current temperature.
| Stream Hs 50°C | = [math]\displaystyle{ \mathbf{\mathit{ \sum \int\limits_{0}^{50}Cp_i.dT }} }[/math] |
| = [math]\displaystyle{ \mathbf{\mathit{(Hs 50^{\circ}C - Hs 0^{\circ}C)}} }[/math] | |
| = [math]\displaystyle{ \mathbf{\mathit{108.46 kJ/kg}} }[/math] (See Table 4 Stream Properties Summary) |
Hz is the enthalpy change (including phase change) from 0°C to current temperature.
| Stream Hz 50°C | = Net Enthalpy @ temperature |
| = [math]\displaystyle{ \mathbf{\mathit{ H_{phase \ change} + \sum \int\limits_{0}^{50}Cp_i.dT}} }[/math] | |
| = [math]\displaystyle{ \mathbf{\mathit{(H final phase - H original phase) 0^{\circ}C + (Hs 50^{\circ}C - Hs 0^{\circ}C)}} }[/math] | |
| = [math]\displaystyle{ \mathbf{\mathit{0 + (108.46 - 0)}} }[/math] (See Table 4 Stream Properties Summary) | |
| = [math]\displaystyle{ \mathbf{\mathit{108.46 kJ/kg}} }[/math] (Note this example contains no phase change) |
Note: For compounds without phase change, you will find that Hs@T = Hz@T. However, for streams involving Steam/Water, where it has [math]\displaystyle{ \mathbf{\mathit{H_lg = 2501\ at\ 0^{\circ}C}} }[/math] & Sat. Pressure, these two terms will not be equal. See Examples on calculating Energy change around a unit for more details.
Stream Entropy values (S)
Stream Entropy values are calculated using the mass weighted mean method. Generally, the Entropy data available are at 25°C. Thus, using these values, stream Entropy (S) at 25°C is calculated.
From Table 3 Species Properties Summary, we have:
| Stream S 25°C | = [math]\displaystyle{ \sum mf_i * S_{i}^{25} }[/math]
| |||
| [math]\displaystyle{ \mathbf{\mathit{= 0.2*0.93 + 0.3*0.70 + 0.4*3.89 + 0.08*0.20 + 0.01*4.86 + 0.01*6.84}} }[/math] | ||||
| [math]\displaystyle{ \mathbf{\mathit{= 2.09 kJ/kg.C}} }[/math] |
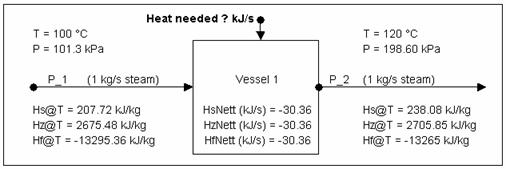
Calculating Energy change around a unit
Calculating Energy change around a unit without phase change
The above is a summary of information you can obtain from SysCAD.
To verify the values using the steam tables (refer to Water and Steam Properties):
- At [math]\displaystyle{ \mathbf{\mathit{100 ^{\circ}C\ at\ sat. P, H_g = 2675.572 kJ/kg}} }[/math]
- At [math]\displaystyle{ \mathbf{\mathit{120 ^{\circ}C\ at\ sat. P, H_g = 2705.9342 kJ/kg}} }[/math]
Thus energy required to heat up the steam for 20°C is:
- [math]\displaystyle{ \mathbf{\mathit{1 kg/s * (2705.9342 - 2675.572) kJ/kg = 30.3622 kJ/s}} }[/math] (i.e. equal to the reported value)
As demonstrated by the above example, you can use Hs (sensible heat), Hz (enthalpy), or Hf (heat of formation) values to calculate the energy required to raise the stream by 20°C.